8. Funciones Inversas.
Sea f una función inyectiva (uno a uno) con dominio A y contradominio B. Entonces su función inversa f-1 tiene dominio B y contradominio A y está definida mediante
f-1(y) = x si y sólo si f(x) = y
para cualquier y en B.
Problema. 71.
|
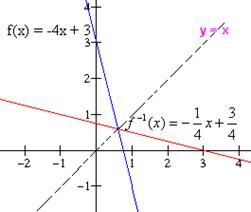
Obtener la inversa de la función f(x) = -4x + 3, y graficar la función f y su inversa. Solución: Por el problema anterior sabemos que f es uno a uno y por lo tanto tiene inversa. Ahora escribimos a f como y = -4x + 3, e intercambiamos las variables x e y para obtener x = -4y + 3. De esta última ecuación despejamos y para obtener la inversa |
|
Problema. 72.
|
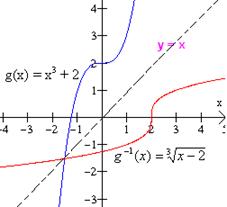
Encontrar la función inversa de g(x) = x3 + 2 y graficar la función g y su inversa. Solución: Primero debemos de mostrar que es uno a uno. Supongamos que f(x1) = f(x2). Es decir que, (x1) 3 + 2 = (x2) 3 + 2. Esto claramente implica que x1 = x2. Para calcular la inversa primero escribimos la función como y = x3 + 2. Luego intercambiamos las variables x y y, para obtener x = y3 + 2. De aquí despejamos la variable y para obtener la inversa. y3 = x -2;
|
|
Problema. 73.
En el problema anterior encontramos que la inversa de la función g(x) = x3 + 2 es![]() . Demuestre que las compuestas (a) (gog-1)(x) = x , y (b) (g-1og)(x) = x
. Demuestre que las compuestas (a) (gog-1)(x) = x , y (b) (g-1og)(x) = x
Solución: (a) (gog-1)(x) = g(g-1(x)) = g(![]() ) = (
) = (![]() )3 + 2 = x – 2 + 2 = x
)3 + 2 = x – 2 + 2 = x
(b) (g-1og)(x) = (g-1(g(x)) = g-1(x3 + 2) = ![]()
Problema. 74.
Encuentre la inversa (si existe) de la función dada por g(x) = 3x2 -2x + 1.
Solución: Una función tiene inversa si ésta cumple con la condición de ser uno a uno. Así primero veremos si la función g dada es uno a uno. Supongamos que si lo es, entonces se debe cumplir la siguiente condición: si g(x1) = g(x2) entonces x1 = x2. Ahora g(x1) = 3(x1)2 -2(x1) + 1, y g(x2) = 3(x2)2 -2(x2) + 1, igualando g(x1) y g(x2) tenemos 3(x1)2 -2(x1) + 1 = 3(x2)2 -2(x2) + 1. Simplificando llegamos a (x1)2 = (x2)2. De aquí obtenemos que x1 = ± x2, lo cual contradice nuestra suposición. Esto demuestra que la función g no es uno a uno. Por consiguiente la función g, no tiene inversa.
Problema. 75.
|
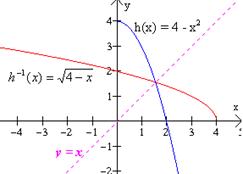
Sea h(x) = 4 - x2. (a) Demostrar que h no es una función uno a uno; (b) restringir el dominio de la función para que sea uno a uno; (c) calcular la inversa en dicho dominio. |
|
|
Solución: (a) Para mostrar que h no es uno a uno, tomemos cualquier valor (distinto de cero) y su negativo, por ejemplo, h(1) = 3 y h(-1) = 3. Puesto que 1 ≠ -1 la definición de uno a uno no se cumple. (b) Si restringimos el dominio únicamente a valores no negativos, es decir, al intervalo [0, +∞), podemos ver en la gráfica que la función es uno a uno. De hecho si x1 y x2 son positivos y h(x1) = h(x2), tenemos, 4 – (x1)2 = 4 – (x2)2 |
|
|
(x1)2 = (x2)2 x1 = x2 ya que ni x1 ni x2 son negativos. Por lo tanto h es uno a uno en este intervalo. (c) Redefinimos la función h(x) = 4 - x2 con dominio [0, +∞), y cuyo rango es el intervalo (-∞, 4], observa la gráfica. Para calcular la inversa primero escribimos la función como y = 4 - x2, después intercambiamos las variables para obtener x = 4 - y2. |
|
|
El paso siguiente es despejar la variable y: x = 4 - y2; x – 4 = -y2; -x + 4 = y2; 4 – x = y2 de donde |
|