7. Funciones Uno a Uno (Inyectivas).

Una función f con dominio A se llama uno a uno (o inyectiva) si no existen dos elementos de A con una misma imagen; es decir:

                                       f(x1) ≠ f(x2)   siempre que x1 ≠ x2.

Otra forma de expresarlo es: F es uno a uno si f(x1) = f(x2)   implica que x1 = x2.

La última frase de la definición anterior significa que:

Una función es uno a uno si y solo si ninguna recta horizontal corta a su gráfica más de una vez.

Problema. 67.              

Determinar si la función m(x) = 2x, es uno a uno.

Solución: Observa que si, calculamos e igualamos m(x1) = (x2), tenemos 2x1 = 2x2. Por lo tanto x1= x2, y por consiguiente la función m es uno a uno.

Problema. 68.              

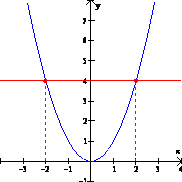
Determinar si la función h(x) = x2 es uno a uno.

Solución: Esta función no es uno a uno. Observa que h(x1) = h(x2) implica que (x1)2 = (x2)2 y por lo tanto, x1 = ± x2, y la función h(x) = x2 no es uno a uno. Por ejemplo, h(2) = 22 = h(-2) = (-2)2 = 4.

Es decir, dados x1 = 2 ≠ x2 = -2, se tiene que h(x1) = h(x2)= 4. En otras palabras dos números distintos x del dominio tienen el mismo valor de y. Observa que cualquier línea horizontal que se trace sobre la curva toca más de un punto de la curva.

Problema. 69.              

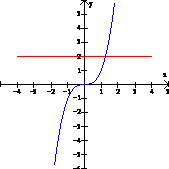
Determinar si la función f(x) = x3 es uno a uno.

Solución: Si x1 ≠ x2, entonces  (dos números diferentes no pueden tener potencias cúbicas iguales). Por lo tanto f(x) = x3 es uno a uno. Observa que cualquier línea horizontal que se trace sobre la curva toca únicamente un punto de ella. x1   x2

Problema. 70.              

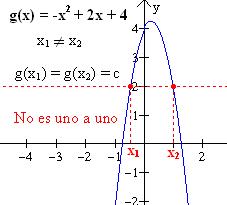
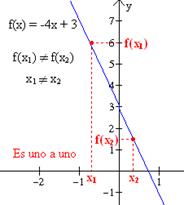
Las gráficas de g(x) = -x2 + 2x + 4 y f(x) = -4x + 3, mostradas indican que hay dos elementos x1 y x2 en el dominio de g, para los cuales g(x1) = g(x2) = c, pero solamente un elemento x1 en el dominio de f para el cual f(x1) = c. por lo tanto, g no es inyectiva pero f sí lo es.