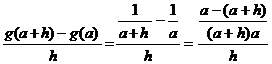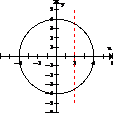1. Definición y Notación Funcional.

Problema. 1.                 

La palabra función se usa con frecuencia para indicar una relación o dependencia de una cantidad respecto de otra, estudia los siguientes ejemplos:

a)      El área de un círculo es una función de su radio. Es decir el área depende del valor del radio.

b)      El volumen de una caja cúbica es una función de la longitud de uno de sus lados. Es decir, el volumen depende del valor de la longitud de uno de sus lados.

c)      La fuerza entre dos partículas con carga eléctrica opuesta es una función de su distancia.

d)     La intensidad del sonido es una función de la distancia desde la fuente sonora.

Problema. 2.                 

La distancia que recorre un avión que viaja a una velocidad de 500 millas por hora (mph) es una función del tiempo de vuelo. Si s representa la distancia en millas y t es el tiempo en horas, entonces la función es:   s (t) = 500t.

Problema. 3.                 

La circunferencia de un círculo es una función de su radio. Esto se suele expresar por medio de la expresión: C(r) = 2πr.

Problema. 4.                 

Los impulsos en las fibras nerviosas viajan a una velocidad de 293 pies/segundo. La distancia recorrida en t segundos está dada por la función: d (t) = 293t.

Problema. 5.                 

Si se sustituye la x por un número en la ecuación y = x³ + 6x² -5, entonces se obtiene un único valor de y. Por lo tanto la ecuación define una función cuya regla es: asigne a un número x en el dominio un único número y tal que y = x³ + 6x² -5. La regla de la función también se puede describir de la siguiente manera f(x) = x³ + 6x² -5.  Por lo tanto: 

 f(0) = 0³ + 6(0)² -5 = -5   y ,

f(2) = 2³ + 6(2)² -5 = 27

Problema. 6.                 

La función
 

es la regla que toma un número, lo divide por 2 y luego le suma 7 al cociente. Si se da un valor para x, ese valor se sustituye en x en la fórmula, y la ecuación se resuelve para f(x), entonces estamos evaluando la función en un valor de su dominio. Por ejemplo, si x = 4,

Si x = 6,                      
 

Problema. 7.                 

Si f(x) = x² + x -2. Calcular f(-x) y –f(x).

f(-x) = (-x)² + (-x) -2 = x²  - x -2

En este caso f (-x) no es lo mismo que –f(x), porque –f(x) es el número negativo de f(x), es decir

-f(x) = -(x² + x -2) = -x² - x +2

Problema. 8.                 

Si x representa el límite de velocidad en millas por hora, entonces el límite de velocidad en kilómetros por hora es una función de x, representada por f(x) = 1.6094x. Si el límite de velocidad en los Estados Unidos es de 55 mph, su equivalente en kilómetros por hora, cuando se redondea al entero más próximo, es

           f(55)  = 1.6094(55) = 89 km/h

Si x = 60 mph,                       f(60)   = 1.6094(60) = 97 km/h

Problema. 9.                 

Sea t el tiempo en segundos y d(t) “la distancia en metros que una piedra cae después de t segundos”. La frase “la distancia que cae la piedra después de t segundos es 5t² metros” se puede escribir como d(t) = 5t². Por ejemplo,

d(1) = 5(1)² = 5

significa “la distancia que la piedra cae después de 1 segundo es 5 metros”

d(4) = 5(4)² = 80

significa “la distancia que la piedra cae después de 4 segundos es 80 metros”

Problema. 10.              

Encuentre el valor de la función f(x) = 2x² – 4x + 1, cuando x = -1, x = 0, y, x = 2.

Solución.

Cuando x = -1, el valor de f está dado por f(-1) = 2(-1)2 – 4(-1) + 1 = 2 + 4 + 1 = 7	Con los datos de la izquierda se puede construir la siguiente tabla: x f(x) -1 7 0 1 2 1
Cuando x = 0, el valor de f está dado por f(0) = 2(0)2 – 4(0) + 1 = 1
Cuando x = 2, el valor de f está dado por f(2) = 2(2)2 – 4(2) + 1= 8 -8 + 1 = 1

Problema. 11.              

Para f (x) = x²-2x, encuentre y simplifique: (a) f (4), (b) f (4 + h),  (c) f (4 + h) – f (4), (d)   

Solución.

(a)    f(4) = 4² – 2(4) = 16 – 8 = 8

(b)   f(4 + h) = (4 + h)² – 2(4 + h) = 16 + 8h + h² – 8 – 2h

                                     = 8 + 6h + h²

(c)    f(4 + h) – f(4) = 8 + 6h + h² – 8 = 6h + h²

(d)   

 

Problema. 12.              

Para g(x) = , encuentre y simplifique

Solución:

Problema. 13.              

Una función se caracteriza geométricamente por el hecho de que toda recta vertical que corta su grafica lo hace exactamente en un solo punto. Si una recta toca más de un punto de la grafica, esta no representa a una función.

(a) No es función.	(b) Si es función.	(c) No es función.
(d) Si es función.	(e) No es función.	(f) Si es función.

Problema. 14.              

¿Cuáles de las siguientes ecuaciones son funciones y por qué?

(a) y = - 2x + 7          (b) y² = x                    (c)  y = x² - 2

(d) x =  2                   (e)   x² + y² = 16         (f) y = 1

Solución:

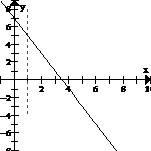
(a) y = -2x + 7 es una función porque para cada valor de la variable independiente x existe un valor y sólo uno de la variable dependiente y. Por ejemplo, si x = - 2(1) + 7 = 5, la gráfica se muestra a la derecha. (b) y2 = x, que es equivalente a y = ±    no es una función porque cada valor positivo de x, hay dos valores de y. Por ejemplo, si y2 = 1, y = ± 1. La gráfica es como la figura del inciso (e) del problema 12.
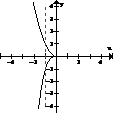
(c) y = x2 - 2 es una función. Para cada valor de x existe un solo valor de y. Ejemplo, si x = - 5, y = 23. Esto no importa mientras también se dé que y = 25 cuando x = 5. La definición de una función simplemente exige que cada valor de x haya un solo valor de y, no, que para cada valor de y hay un solo valor de x. La gráfica sería como la figura (f), del problema 12. Demostrando que una parábola con eje paralelo al eje de las y es una función.
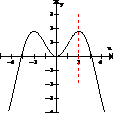
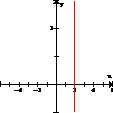
(d) x = 2 no es una función. La gráfica de x = 2 es una línea vertical. Esto significa que en x = 2, y tiene muchos valores. La gráfica se muestra a la derecha. (e) x² + y² = 16 no es una función. Si x = 0, y² = 16 y y = + 4. La gráfica es un círculo, similar a la figura (a) del problema 12. Un círculo no pasa la prueba de línea vertical.
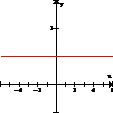
(f) y = 1 es una función. La grafica de y = 1 es una línea horizontal. Esto significa que al valor de y = 1 se le asignan muchos valores de x. La grafica se muestra a la derecha.