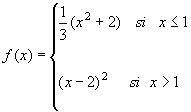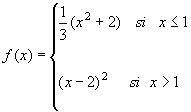1.3 Una función no derivable en un punto
En la siguiente escena se muestra la gráfica de la función,
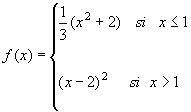
y la recta secante para x = -2 y h = 0.00001, es
decir una muy buena aproximación a la recta tangente en el punto.
Los
valores de h, controlables con el selector, son solamente -0.00001
y 0.00001,
Con el fin de reconocer visualmente los puntos
de derivabilidad y no derivabilidad, atienda las instrucciones que se presentan
en la parte derecha de la escena.
|
|
- Asigne a x cualquier valor diferente de uno y oprima el selector de h.
Se alternarán los valores de
-0.000001 y 0.000001, no apreciándose cambios significativos en la
rectas secantes, por lo próximo de estos valores. Esto significa que las rectas
secantes se aproximan a una misma recta, la recta tangente; es decir, la función es derivable en
este punto.
- Sin embargo si se posiciona en x = 1, y
alterna los valores de h, observará cambios abruptos en la rectas
secantes, a pesar de lo próximo de los valores de h. Esto significa
que no existe una única recta a la cual se parezcan estas secantes; es decir, la
función no tiene recta tangente en este punto o bien la función no es
derivable en x = 1. También podemos decir que la gráfica no es una
curva suave en las cercanías de este punto.
|
A continuación se presenta una escena, en la cual se
muestra la recta tangente en cada punto. Mantenga oprimido el selector del
control x, para apreciar la relación entre la recta tangente y la
curva..
|
|
- Oprimiendo el selector, asigne a x cualquier valor diferente
de uno. Observará que existe una recta tangente en cada uno de
estos puntos, lo cual significa que la función es derivable en
estos puntos.
Apreciará también que la curva y la recta son prácticamente
indistinguibles en las cercanías del punto de tangencia, lo cual nos
permite afirmar que, en la región de derivabilidad, se trata de una curva
suave.
- En x = 1 no existe la recta tangente, lo cual significa que la
función no es derivable en este punto.
En general, en los puntos de no derivabilidad no existe una recta a la
cual la curva "se pegue", por lo que se pierde la
condición local de suavidad al darse un cambio abrupto
en su trayectoria.
|
Construcción del Trazador
de Derivadas