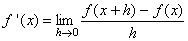1. El Concepto de Derivada
A lo largo de este trabajo, como se mencionó en los objetivos, se supondrá que el alumno está familiarizado
con la definición de derivada como un límite y con su interpretación geométrica como la
pendiente de la recta tangente. En esta sección, recordamos la definición y
utilizamos el Applet DESCARTES para simular lo que el profesor hace en el
pizarrón, al presentar la interpretación geométrica de la derivada.
Definición:
Se dice que la función f es derivable en el punto x, si el
siguiente límite existe.
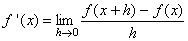
Al
valor de este límite le llamamos LA DERIVADA de f en el punto x.
Recuerde que tomar límite cuando h
tiende a cero, significa que h es diferente de cero pero
tan pequeño como se
quiera, independientemente del signo.
Cuando la función
es derivable en x, es decir que el límite existe, es indistinto
obtener la aproximación a la pendiente de la recta tangente con valores
positivos o negativos de h, con tal de que éstos sean muy pequeños.
A excepción de la parte correspondiente a la
derivada de algunas funciones especiales, este trabajo analiza funciones
derivables en todo punto, lo que justifica que el cociente de
diferencias aproxime a la derivada de la función, para valores de h
muy pequeños. Por ello, para efectos didácticos, consideramos valores
pequeños de h y siempre positivos.
Con el fin de recrear la interpretación geométrica de este concepto,
sigamos las instrucciones que se presentan en la siguiente escena, por medio del
control "Pasos". En el paso 0 se muestra la gráfica de la función
f (x)
= x2 y los valores de x = 0.5 y
h = 1.5. A partir de esto, se presentan gráficamente los elementos que aparecen
en la definición de derivada.
Para
efectos de visualización gráfica, supondremos que el
cociente de diferencias es aproximadamente igual al valor de la derivada, es
decir:
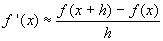
para
valores "muy pequeños de h".
1.1 Aproximándonos con h positiva
Obsérvese que nos estamos aproximando a la recta tangente
tomando valores positivos muy pequeños de h . Como mencionamos
anteriormente, si la función es derivable, deberiamos también poder poder
hacerlo para valores negativos muy pequeños de h .
Aproximándonos
con h negativa
1.2
Aproximándonos
con h negativa
En la siguiente escena mostramos de nuevo la derivada de f(x)
= x2 para valores negativos de
h.
Un ejemplo de una función no derivable
en un punto