Límites laterales

Hasta el momento hemos visto límites de funciones cuyo trazo es continuo, sin cortes o saltos bruscos. Sin embargo, existen algunas funciones que presentan algunas discontinuidades, llamadas funciones discontinuas y que estudiaremos en el tema continuidad de funciones. Nos dedicaremos ahora a estudiar los límites en este tipo de funciones.
Consideremos la siguiente representación gráfica de una función $f$, en la que existe una discontinuidad cuando $x=a$:

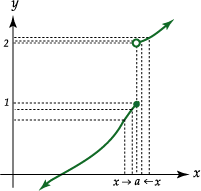notemos que cuando $x$ tiende hacia "a" por la derecha de "a" la función tiende a 2, pero cuando $x$ tiende hacia "a" por la izquierda de "a", la función tiende hacia 1.

Escribimos $x\Rightarrow a^{+}$ para indicar que $x$ tiende hacia "a" por la derecha, es decir, tomando valores mayores que "a". Similarmente $x\Rightarrow a^{-}$ indica que $x$ tiende hacia "a" por la izquierda, o sea, tomando valores menores que "a". Utilizando ahora la notación de límites, escribimos $\displaystyle {\lim_{x \rightarrow{a^{+}}}{f(x)}=2}$ y $\displaystyle {\lim_{x \rightarrow{a^{-}}}{f(x)}=1}$. Estos límites reciben
el nombre de límites laterales; el límite por la derecha es 2 y el límite por la izquierda es 1.
Ejemplo:
Determinaremos los límites en los puntos de discontinuidad de la función $h$ cuya representación gráfica es la siguiente:

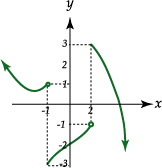Se tiene que:
$\displaystyle {\lim_{x \rightarrow{2^{+}}}{h(x)}=3}$ y $\displaystyle {\lim_{x \rightarrow{2^{-}}}{h(x)}=-1}$
$\displaystyle {\lim_{x \rightarrow{-1^{+}}}{h(x)}=-3}$ y $\displaystyle {\lim_{x \rightarrow{-1^{-}}}{h(x)}=1}$

Definición de límites laterales o unilaterales  

 

Definición de límite por la derecha

 

 

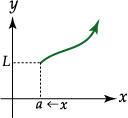
Se dice que $\displaystyle {\lim_{x \rightarrow{a^{+}}}{f(x)}=L}$ si y solo si para cada $\varepsilon >0$ existe $\delta >0$ tal que si $0<x-a<\delta$ entonces $\vert f(x)-L\vert<\varepsilon \;\; L$ es el límite por la derecha de $f(x)$ en "a".  

   

Observe que no hay barras de valor absoluto alrededor de $x-a$, pues $x-a$ es mayor que cero ya que $x>a$.

 

Definición de límite por la izquierda

 

 

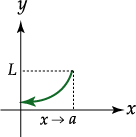
Se dice que $\displaystyle {\lim_{x \rightarrow{a^{-}}}{f(x)}=R}$ si y solo si para cada $\varepsilon >0$ existe $\delta >0$ tal que si $0<a-x<\delta$ entonces $\vert f(x)-R\vert<\varepsilon\cdot R$ es el límite por la izquierda de $f(x)$ en "a".  

Note que la expresión $a-x$ es mayor que cero, pues $x\rightarrow a^{-}$ por lo que $x<a$.

En adelante determinaremos los límites laterales a partir de la representación gráfica de una función cuya ecuación se da.
Ejemplo:
Determinar los límites, en los puntos de discontinuidad, de la función $f$ definida por:
$f(x)=\left\{ \begin{array}{ccc} x+2 & \mbox{si} & x\geq 1 \\ -x^{2}-1 & \mbox{si} & x<1 \end{array}\right.$
Primero hagamos la gráfica de la función:

 

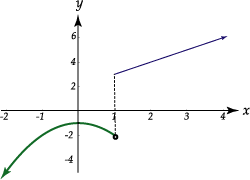
El punto de discontinuidad se presenta cuando $x=1$

Luego: $\displaystyle {\lim_{x \rightarrow{1^{+}}}{f(x)}=3}$ y $\displaystyle {\lim_{x \rightarrow{1^{-}}}{f(x)}=-2}$
Observe que el límite por la derecha (3), es diferente al límite por la izquierda (2).
Ejercicio:
Represente la función $h$ definida por $h(x)=\left\{ \begin{array}{ccc} x-1 & \mbox{si} & x<0 \\ x+1 & \mbox{si} & x>0 \end{array}\right.$
y determine los límites laterales en el punto de discontinuidad.

Es posible demostrar que para que exista $\displaystyle {\lim_{x \rightarrow{a}}{f(x)}}$ es necesario y suficiente que los límites laterales existan y sean iguales.
Es decir, $\displaystyle {\lim_{x \rightarrow{a}}{f(x)}=L}$ si y solo si $\displaystyle {\lim_{x \rightarrow{a^{+}}}{f(x)}=L}$ y $\displaystyle {\lim_{x \rightarrow{a^{-}}}{f(x)}=L}$

Por consiguiente, si $\displaystyle {\lim_{x \rightarrow{a^{+}}}{f(x)}}$ es diferente de $\displaystyle {\lim_{x \rightarrow{a^{-}}}{f(x)}}$ se dice que $\displaystyle {\lim_{x \rightarrow{a}}{f(x)}}$ no existe.
Ejemplo:
Representemos gráficamente la función definida por:

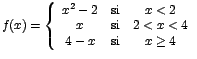
$f(x)=\left\{ \begin{array}{ccc} x^{2}-2 & \mbox{si} & x<2 \\ x & \mbox{si} & 2<x<4 \\ 4-x & \mbox{si} & x\geq 4 \end{array}\right.$

 

Como $\displaystyle {\lim_{x \rightarrow{2^{+}}}{f(x)}=2}$ y $\displaystyle {\lim_{x \rightarrow{2^{-}}}{f(x)}=2}$, entonces $\displaystyle {\lim_{x \rightarrow{2}}{f(x)}=2}$

Como $\displaystyle {\lim_{x \rightarrow{4^{+}}}{f(x)}=0}$ y $\displaystyle {\lim_{x \rightarrow{4^{-}}}{f(x)}=4}$, entonces $\displaystyle {\lim_{x \rightarrow{4}}{f(x)}}$ no existe.
Ejercicio:
Considere la representación gráfica de la función $g$ definida por:
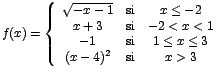
$f(x)=\left\{ \begin{array}{ccc} \sqrt{-x-1} & \mbox{si} & x\leq -2 \\ x+3 & ... ...& \mbox{si} & 1\leq x\leq 3 \\ (x-4)^{2} & \mbox{si} & x>3 \end{array}\right.$
De$\displaystyle {\lim_{x \rightarrow{-2}}{g(x)}}$termine si existen cada uno de los límites siguientes:

a.
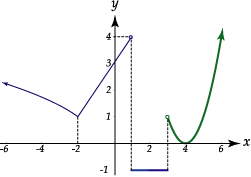b.$\displaystyle {\lim_{x \rightarrow{1}}{g(x)}}$
c.$\displaystyle {\lim_{x \rightarrow{3}}{g(x)}}$
d.$\displaystyle {\lim_{x \rightarrow{4}}{g(x)}}$
e.$\displaystyle {\lim_{x \rightarrow{0}}{g(x)}}$