Indeterminaciones

Indeterminaciones.

En algunos límites no es posible aplicar directamente los teoremas sobre límites, especialmente el del límite de un cociente de funciones, ya que se presenta la forma indeterminada $\displaystyle {\frac{0}{0}}$ .
En estos casos se hace necesario realizar primero algún proceso algebraico, para luego determinar el valor del límite.
Es indispensable en esta parte tener muy en claro los conceptos sobre factorización, racionalización y valor absoluto.
Por medio de ejemplos estudiaremos:

a.	Límites que involucran factorizaciones

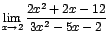
1.	$\displaystyle {\lim_{x \rightarrow{2}}{\frac{2x^{2}+2x-12}{3x^{2}-5x-2}}}$

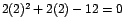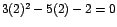
Si evaluamos el numerador se obtiene: $2(2)^{2}+2(2)-12=0$ y en el denominador: $3(2)^{2}-5(2)-2=0$
Luego se tiene la expresión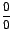 $\displaystyle {\frac{0}{0}}$ que no tiene sentido.
Como 2 hace cero ambos polinomios podemos hacer una factorización como sigue: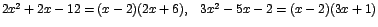 $2x^{2}+2x-12=(x-2)(2x+6),\;\;\;3x^{2}-5x-2=(x-2)(3x+1)$
Luego el límite dado puede escribirse

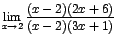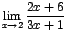como $\displaystyle {\lim_{x \rightarrow{2}}{\frac{(x-2)(2x+6)}{(x-2)(3x+1)}}}$ , y simplificando se obtiene: $\displaystyle {\lim_{x \rightarrow{2}}{\frac{2x+6}{3x+1}}}$ que sí puede determinarse pues 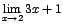$\displaystyle {\lim_{x \rightarrow{2}}{3x+1}}$ es diferente de cero.

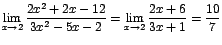
Luego: $\displaystyle {\lim_{x \rightarrow{2}}{\frac{2x^{2}+2x-12}{3x^{2}-5x-2}}=\lim_{x \rightarrow{2}}{\frac{2x+6}{3x+1}}=\frac{10}{7}}$

2.	$\displaystyle {\lim_{x \rightarrow{-1}}{\frac{x^{3}+(1-a)x^{2}-ax}{x^{2}-x-2}}}$

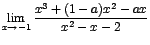
Evaluando nuevamente numerador y denominador se obtiene:
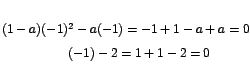
Puede escribirse el límite anterior ya factorizados los polinomios como: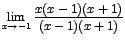

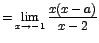$\displaystyle {\lim_{x \rightarrow{-1}}{\frac{x(x-1)(x+1)}{(x-1)(x+1)}}}$ $=\displaystyle {\lim_{x \rightarrow{-1}}{\frac{x(x-a)}{x-2}}}$ simplificando la expresión anterior.

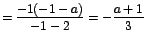$=\displaystyle {\frac{-1(-1-a)}{-1-2}=-\frac{a+1}{3}}$ .

b.	Límites que involucran racionalizaciones

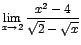
1.	$\displaystyle {\lim_{x \rightarrow{2}}{\frac{x^{2}-4}{\sqrt{2}-\sqrt{x}}}}$

Como al evaluar el numerador y el denominador se obtiene cero en ambos, procedemos a racionalizar el denominador de la forma siguiente:

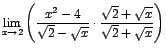
$\displaystyle {\lim_{x \rightarrow{2}}{\left(\frac{x^{2}-4}{\sqrt{2}-\sqrt{x}}\cdot \frac{\sqrt{2}+\sqrt{x}}{\sqrt{2}+\sqrt{x}}\right)}}$
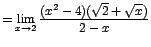
$=\displaystyle {\lim_{x \rightarrow{2}}{\frac{(x^{2}-4)(\sqrt{2}+\sqrt{x})}{2-x}}}$
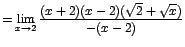
$=\displaystyle {\lim_{x \rightarrow{2}}{\frac{(x+2)(x-2)(\sqrt{2}+\sqrt{x})}{-(x-2)}}}$
$=\displaystyle {\lim_{x \rightarrow{2}}{[-(x+2)(\sqrt{2}+\sqrt{x})]}}$
en este último límite no hay ningún problema y aplicando los teoremas respectivos se obtiene como resultado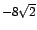 $-8\sqrt{2}$

Como vuelve a presentarse la forma 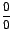$\displaystyle {\frac{0}{0}}$ , procedemos a racionalizar como sigue: $\displaystyle {\lim_{x \rightarrow{3}}{\frac{\sqrt[3]{x^{2}+6x}-3}{x-3}\cdot \f... ...\sqrt[3]{x^{2}+6x}+3^{2}}{\sqrt[3]{(x^{2}+6x)^{2}}+3\sqrt[3]{x^{2}+6x}+3^{2}}}}$ $\displaystyle {\lim_{x \rightarrow{3}}{\frac{(\sqrt[3]{x^{2}+6x})^{3}-3^{3}}{(x-3)\left[\sqrt[3]{(x^{2}+6x)^{2}}+3\sqrt[3]{x^{2}+6x}+9\right]}}}$ $\displaystyle {\lim_{x \rightarrow{3}}{\frac{(x-3)(x+9)}{(x-3)\left[\sqrt[3]{(x^{2}+6x)^{2}}+3\sqrt[3]{x^{2}+6x}+9\right]}}}$

$\displaystyle {\lim_{x \rightarrow{3}}{\frac{x+9}{\sqrt[3]{(x^{2}+6x)^{2}}+3\sqrt[3]{x^{2}+6x}+9}}=\frac{4}{9}}$

c.	Límites con valor absoluto

Recuerde que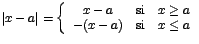 $\vert x-a\vert=\left\{\begin{array}{ccc} x-a & \mbox{si} & x\geq a \\ -(x-a) & \mbox{si} & x\leq a \end{array} \right.$

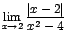
1.	$\displaystyle {\lim_{x \rightarrow{2}}{\frac{\vert x-2\vert}{x^{2}-4}}}$

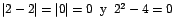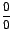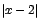Como $\vert 2-2\vert=\vert\vert=0\;\;\mbox{y}\;\;2^{2}-4=0$ vuelve a obtenerse la forma $\displaystyle {\frac{0}{0}}$ . Como aparece $\vert x-2\vert$ de acuerdo a la definición de valor absoluto se tiene que: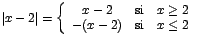

$\vert x-2\vert=\left\{\begin{array}{ccc} x-2 & \mbox{si} & x\geq 2 \\ -(x-2) & \mbox{si} & x\leq 2 \end{array} \right.$
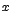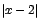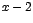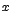Así, para valores de mayores que 2 la expresión $\vert x-2\vert$ se puede sustituir por , y para valores de mayores que 2 se sustituye por 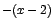, por lo que se hace necesario calcular los límites cuando $x\rightarrow 2^{+}\;\;\mbox{y cuando}\;\;x\rightarrow 2^{-}$ , es decir, se deben calcular los límites laterales. Luego:
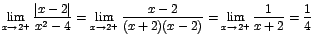
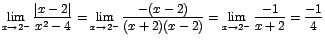
$\displaystyle {\lim_{x \rightarrow{2^{+}}}{\frac{\vert x-2\vert}{x^{2}-4}}=\lim... ...\frac{x-2}{(x+2)(x-2)}}=\lim_{x \rightarrow{2^{+}}}{\frac{1}{x+2}}=\frac{1}{4}}$ $\displaystyle {\lim_{x \rightarrow{2^{-}}}{\frac{\vert x-2\vert}{x^{2}-4}}=\lim... ...{-(x-2)}{(x+2)(x-2)}}=\lim_{x \rightarrow{2^{-}}}{\frac{-1}{x+2}}=\frac{-1}{4}}$
Como los límites laterales son diferentes entonces el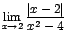 $\displaystyle {\lim_{x \rightarrow{2}}{\frac{\vert x-2\vert}{x^{2}-4}}}$ no existe.

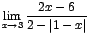
2.	$\displaystyle {\lim_{x \rightarrow{3}}{\frac{2x-6}{2-\vert 1-x\vert}}}$

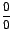Vuelve a presentarse la forma $\displaystyle {\frac{0}{0}}$ . Analizando el valor absoluto se obtiene que:
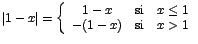
$\vert 1-x\vert=\left\{\begin{array}{ccc} 1-x & \mbox{si} & x\leq 1 \\ -(1-x) & \mbox{si} & x>1 \end{array} \right.$
Como se desea averiguar el límite cuando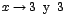 $x\rightarrow 3\;\;\mbox{y}\;\;3$ es mayor que 1, entonces se analiza únicamente el siguiente límite:
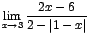
$\displaystyle {\lim_{x \rightarrow{3}}{\frac{2x-6}{2-\vert 1-x\vert}}}$
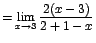
$=\displaystyle {\lim_{x \rightarrow{3}}{\frac{2(x-3)}{2-[-(1-x)]}}}$
$=\displaystyle {\lim_{x \rightarrow{3}}{\frac{2(x-3)}{2+1-x}}}$
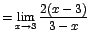
$=\displaystyle {\lim_{x \rightarrow{3}}{\frac{2(x-3)}{3-x}}}$
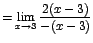
$=\displaystyle {\lim_{x \rightarrow{3}}{\frac{2(x-3)}{-(x-3)}}}$
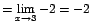
$=\displaystyle {\lim_{x \rightarrow{3}}{-2}=-2}$
En este caso el límite sí existe.

d.	Límites que involucran un cambio de variable

1.	$\displaystyle {\lim_{y \rightarrow{0}}{\frac{\sqrt[3]{1+y}-1}{1-\sqrt{1+y}}}}$

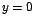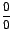Al evaluar numerador y denominador en se obtiene $\displaystyle {\frac{0}{0}}$ . Aunque en este caso podría efectuarse una racionalización, el procedimiento sería muy largo pues hay que racionalizar tanto el numerador como el denominador. Por tanto, vamos a hacer un cambio de variable en la forma siguiente.
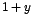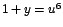Se desea sustituir la expresión por otra que tenga tanto raíz cúbica como raíz cuadrada. Luego, sea $1+y=u^{6}$ (observe que $\sqrt[6]{u}=c^{3}\;\;\mbox{y}\;\;\sqrt[3]{u^{6}}=u^{2}$ ).
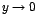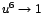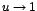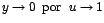Además cuando $y\rightarrow 0$ se tiene que $u^{6}\rightarrow 1$ y por tanto $u\rightarrow \sqrt[6]{1}$ , es decir, $u\rightarrow 1$ ; en el límite original se sustituye $y\rightarrow 0\;\;\mbox{por}\;\;u\rightarrow 1$ Sustituyendo se tiene que:
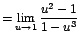
$\displaystyle {\lim_{y \rightarrow{0}}{\frac{\sqrt[3]{1+y}-1}{1-\sqrt{1+y}}}}$ $=\displaystyle {\lim_{u \rightarrow{1}}{\frac{\sqrt[3]{u^{6}}-1}{1-\sqrt{u^{6}}}}}$ $=\displaystyle {\lim_{u \rightarrow{1}}{\frac{u^{2}-1}{1-u^{3}}}}$
Aunque vuelve a presentarse la forma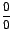 $\displaystyle {\frac{0}{0}}$ , la expresión ahora es fácilmente factorizable. Así:
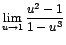
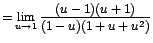
$\displaystyle {\lim_{u \rightarrow{1}}{\frac{u^{2}-1}{1-u^{3}}}}$ $=\displaystyle {\lim_{u \rightarrow{1}}{\frac{(u-1)(u+1)}{(1-u)(1+u+u^{2})}}}$
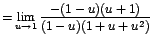
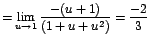
$=\displaystyle {\lim_{u \rightarrow{1}}{\frac{-(1-u)(u+1)}{(1-u)(1+u+u^{2})}}}$ $=\displaystyle {\lim_{u \rightarrow{1}}{\frac{-(u+1)}{(1+u+u^{2})}}=\frac{-2}{3}}$

2.	$\displaystyle {\lim_{x \rightarrow{1}}{\frac{\sqrt[5]{3-2x}-1}{1-x}}}$

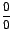
Nuevamente, evaluando el numerador y el denominador en 1 se obtiene $\displaystyle {\frac{0}{0}}$
En este caso vamos a sustituir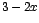 por una expresión que posea raíz quinta. Tomamos entonces $3-2x=u^{5}\;\;\mbox{pues}\;\;\sqrt[5]{u^{5}}=u$ .
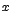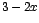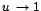
Cuando tiende a 1 se tiene que también tiende a 1 y por tanto $u^{5}\rightarrow 1\;\;\mbox{y}\;\;u\rightarrow \sqrt[5]{1}$ de donde $u\;\rightarrow 1$
Sustituyendo se obtiene que:
$\displaystyle {\lim_{x \rightarrow{1}}{\frac{\sqrt[5]{3-2x}-1}{1-x}}}$ $=\displaystyle {\lim_{u \rightarrow{1}}{\frac{\sqrt[5]{u^{5}}-1}{1-\frac{3-u^{5}}{2}}}}$
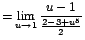
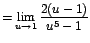
$=\displaystyle {\lim_{u \rightarrow{1}}{\frac{u-1}{\frac{2-3+u^{5}}{2}}}}$ $=\displaystyle {\lim_{u \rightarrow{1}}{\frac{2(u-1)}{u^{5}-1}}}$
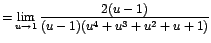
$=\displaystyle {\lim_{u \rightarrow{1}}{\frac{2(u-1)}{(u-1)(u^{4}+u^{3}+u^{2}+u+1)}}}$
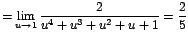
$=\displaystyle {\lim_{u \rightarrow{1}}{\frac{2}{u^{4}+u^{3}+u^{2}+u+1}}=\frac{2}{5}}$