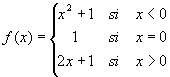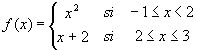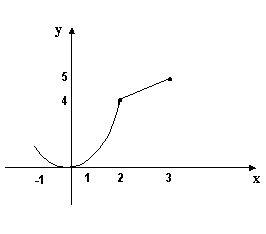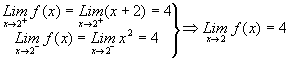fig. 8.6.
Al mirar con un poco de
cuidado las gráficas de la fig. 8.6., se pueden deducir intuitivamente,
resultados que permitirán comprender con mayor claridad la definición
precisa de lo que significa: "ser una función continua en un punto dado de
su dominio".
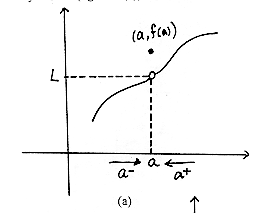
En la gráfica de la fig. 8.6. (a) se
tiene:
i.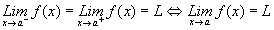 .
(Existe).
.
(Existe).
ii. f(a) existe.
Pero,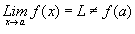 .
(Por esta razón f es discontinua) ¿Qué le sucede a la gráfica si
f(a)= L?
.
(Por esta razón f es discontinua) ¿Qué le sucede a la gráfica si
f(a)= L?
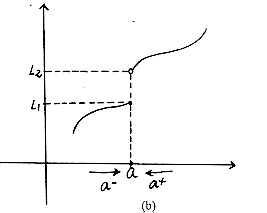
Para la gráfica de la fig. 8.6. (b) se tiene:
i.
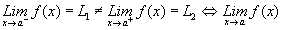 No
existe. (Por esta razón f es discontinua)
No
existe. (Por esta razón f es discontinua)
ii. f(a) = L1(Existe).
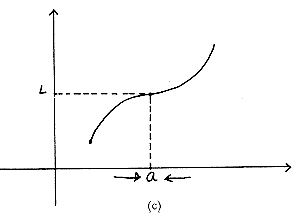
Finalmente, para la gráfica de la fig. 8.6. (c) se tiene:
i.
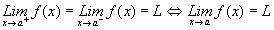 .
(Existe).
.
(Existe).
(Por esta razón f es discontinua)
ii. f(a) (Existe).
iii.
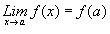
Estas tres condiciones son las que en última instancia, permiten deducir
intuitivamente que la función cuya gráfica aparece en la fig. 8.6. (c) es
continua en el punto a.
Lo anterior nos permite establecer la siguiente definición.
Definición:
Una función f es CONTINUA EN x =
a, si y solo si se satisfacen
las siguientes condiciones:
i. f(a) existe.
ii.
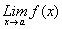 existe.
existe.
iii.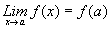
Si al menos una de estas tres condiciones deja de cumplirse se dice que
f es DISCONTINUA (NO CONTINUA) en x =
a.
Observaciones:
i. Si en la definición anterior,
sustituimos
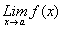 por
por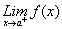 o por
o por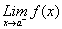 ,
se dice entonces que f es continua a la derecha,
respectivamente, a la izquierda del punto x =
a.
,
se dice entonces que f es continua a la derecha,
respectivamente, a la izquierda del punto x =
a.
ii. Algunos autores adoptan como
definición de continuidad en un punto, la condición iii. de la definición
anterior, esto es, f es continua en x =
a, si y solo si,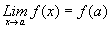 .
.
iii. Si en la definición de
continuidad se hace: x = a + h;
con a y (a
+ h) en el dominio de f, se dice entonces, que f es
continua en a si y solo si,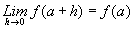 .
.
iv. Si f es discontinua en
x = a y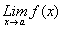 existe pero es diferente de f(a),
se dice que la discontinuidad es REMOVIBLE O EVITABLE. En caso
contrario, se dice que la discontinuidad es ESENCIAL.
existe pero es diferente de f(a),
se dice que la discontinuidad es REMOVIBLE O EVITABLE. En caso
contrario, se dice que la discontinuidad es ESENCIAL.
Asi por ejemplo, la gráfica de la fig. 8.6. (a) corresponde a la gráfica
de una función con discontinuidad Removible o evitable en
x = a. Mientras que la gráfica de
la fig. 8.6. (b) corresponde a la gráfica de una función con
discontinuidad ESENCIAL en x = a.
v. Cuando una función tiene
discontinuidad removible en un punto, se usa la frase "Remover la
discontinuidad" para indicar que se puede redefinir la función haciendo
que:
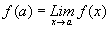 y de esta manera obtener una nueva función continua en x =
a.
Considere por ejemplo, la función f
definida por:
y de esta manera obtener una nueva función continua en x =
a.
Considere por ejemplo, la función f
definida por:
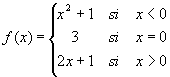
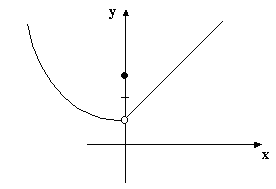
La gráfica de la función aparece en la fig. 8.7.
fig. 8.7.
Si se analiza la
continuidad de f en el punto x = 0, se tiene:
i.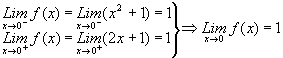 (Existe)
(Existe)
ii.f (0) = 3 (Existe)
Pero,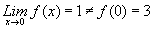 ;
lo que indica que f es discontinua en x = 0. Ahora, como
;
lo que indica que f es discontinua en x = 0. Ahora, como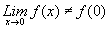 ,
la discontinuidad es evitable.
,
la discontinuidad es evitable.
Se puede entonces, "remover" o "evitar" la discontinuidad,
redefiniendo una nueva función de tal forma que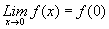 .
Esto es, redefiniendo a f asi:
.
Esto es, redefiniendo a f asi:
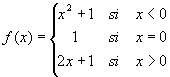
Esta nueva función es
continua en x = 0.
Es de anotar que la función f se ha redefinido y por lo tanto, no
se trata de la misma función. ¿Porqué?
8.3.1. Teoremas sobre funciones
continuas. Los siguientes
teoremas, que se enuncian sin demostración, señalan importantes
propiedades de las funciones continuas y son al mismo tiempo herramientas
útiles que permiten deducir, en muchos casos, la continuidad de una
función, sin recurrir directamente al empleo de la definición.
TEOREMA 1. (Algebra de funciones continuas)
Sean f, g dos
funciones continuas en el punto x = a.
Entonces:
i. (f + g) es continua en
x = a. (Suma de funciones
continuas es continua).
ii. (f – g) es continua en
x = a. (Diferencia de funciones
continuas es continua).
iii. (f ×
g) es continua en x =
a. (Producto de funciones
continuas es continua).
iv. 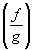 es continua en x =
a, si g(a)
¹ 0. (Cociente de funciones continuas es
continua).
es continua en x =
a, si g(a)
¹ 0. (Cociente de funciones continuas es
continua).
Consecuencias:
C.C.1. La función polinómica es continua en
todo punto del eje real. En efecto, sea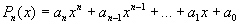 una función polinómica de grado n.
una función polinómica de grado n.
Sea a un punto cualquiera del eje real. Al
aplicar sucesivamente el teorema 1 en sus partes i., ii. y iii se
obtiene que:
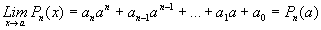 y de aquí, Pn (x) es una función continua en todo
punto del eje real.
y de aquí, Pn (x) es una función continua en todo
punto del eje real.
C.C.2. Toda función racional es continua en
los puntos que no anulen el denominador de la función.
Demostración: aplicar el teorema 1.
TEOREMA 2. (Límite de la función compuesta)
Sean f y g dos funciones tales que: f
es continua en b y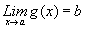 .
Entonces:
.
Entonces: 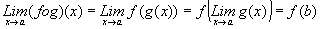 .
.
Algunas consecuencias importantes de este teorema son las siguientes:
C.C.3. Si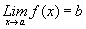 ,
entonces,
,
entonces,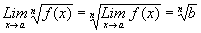 .
Cuando n sea par, se debe cumplir además que b > 0.
.
Cuando n sea par, se debe cumplir además que b > 0.
C.C.4. Si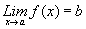 ,
entonces,
,
entonces,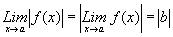
Las consecuencias C.C.3. y C.C.4., se expresan
respectivamente en palabras de la siguiente forma: "El límite de la raiz
n-sima, es la raiz n-sima del límite y "El límite del valor absoluto, es
el valor absoluto del límite".
C.C.5. (Continuidad de la función compuesta).
Si g es continua en a y f es continua en
g(a), entonces (f o g) (x) = f (g(x)) es continua en a.
8.3.2. Continuidad En Un
Intervalo
Definiciones:
i. Una función f es continua
en un INTERVALO ABIERTO si y solo si, f es continua en TODO
punto del intervalo.
ii.Una función f es continua
en un INTERVALO CERRADO [a, b] si y solo si, f es continua
en el intervalo abierto (a, b), continua por la derecha de a
y continua por la izquierda de b.
Definiciones similares
se establecen para la continuidad de una función en un intervalo
semiabierto de cualquiera de las formas: (a, b] ó [a, b).
Asi por ejemplo, la
función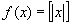 (mayor entero menor o igual a x), es continua en los intervalos de
la forma
(mayor entero menor o igual a x), es continua en los intervalos de
la forma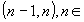 ü
, ya que en cada uno de estos intervalos, la función es constante.
ü
, ya que en cada uno de estos intervalos, la función es constante.
Considere también la función f definida por:
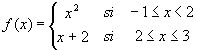
y cuya gráfica aparece en la fig. 8.8.
Se desea analizar la continuidad de f en el intervalo [-1, 3]
fig. 8.8.
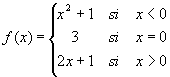
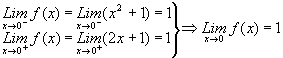 (Existe)
(Existe)