4. Gráficas y Transformaciones.
Sea f(x) una función y c e Df.
A. Traslaciones verticales.
Si c > 0, entonces la grafica de f(x) + c es una traslación de f, c unidades hacia arriba.
Si c < 0, entonces la grafica de f(x) + c es una traslación de f, c unidades hacia abajo.
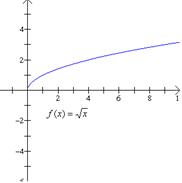
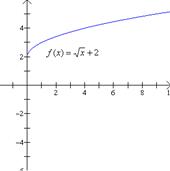
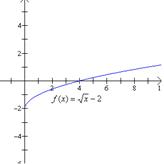
Problema. 47.
|
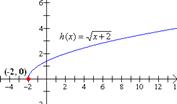
Encontrar la gráfica de (a) Solución: Observa que los incisos (b) y (c) son una traslación vertical de la función |
||
|
|
|
|
B. Traslaciones horizontales.
Si c > 0, entonces la grafica de f(x-c) es una traslación de f, c unidades hacia la derecha.
Si c < 0, entonces la grafica de f(x-c) es una traslación de f, c unidades hacia la izquierda.
Problema. 48.
Grafica las siguientes funciones (a) ![]() , (b)
, (b) ![]() , (c)
, (c) ![]()
|
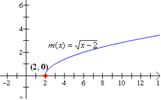
Solución: Observa que los incisos (b) y (c) son una traslación horizontal de la función |
||
|
|
|
|
C. Expansiones y Contracciones
Si c > 1, entonces la gráfica de cf(x), es un alargamiento vertical de la gráfica de f por un factor de c unidades.
Si 0 < c < 1, entonces la gráfica de cf(x), es una reducción vertical de la gráfica de f por un factor de c unidades.
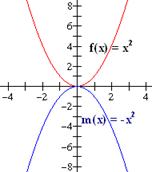
Si c < 0 entonces cf(x) es una reflexión sobre el eje x de la función f.
Problema. 49.
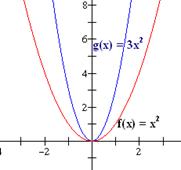
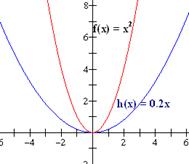
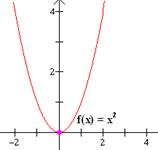
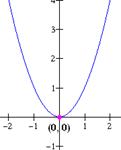
Grafica las siguientes funciones: (a) f(x) = x2, (b) g(x) = 3x2, (c) h(x) = 0.2x, (d) m(x) = -x2.
Solución: La grafica de f es una parábola que se abre hacia arriba y tiene su vértice en el eje x. (b) La gráfica de g es un alargamiento vertical de la función f por factor de 3; (c) la gráfica de h es una reducción vertical de f por factor de 0.5; (d) la gráfica de m es una reflexión de f sobre el eje x. Las gráficas se muestran abajo.
|
|
|
|
Problema. 50.
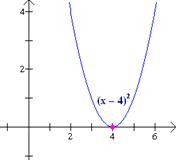
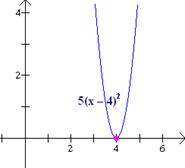
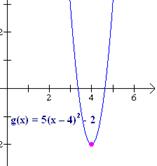
Graficar g(x) = 2(x – 4)2 – 2, utilizando transformaciones.
Solución: Observa que la función g se puede obtener a partir de la función f(x) = x2 e tres pasos: g(x) = 5(x – 4)2 - 2
![]()
El primer paso traslada la grafica de f horizontalmente 4 unidades hacia la derecha; el paso 2, alarga verticalmente la función f desde el eje x por un factor de 2; el paso 3 traslada a la función f 3 unidades hacia abajo. Los pasos gráficos y la grafica de g se muestran abajo.
|
|
|
|
f(x) = x2 |
Paso 1 |
|
|
|
|
Paso 2 |
Paso 3 |
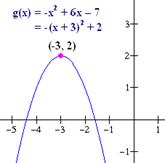
Problema. 51.
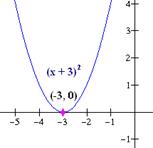
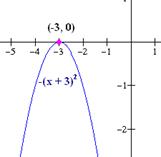
Trazar la gráfica de la función g(x) = -x2 + 6x – 7, utilizando transformaciones.
Solución: Primero completamos el cuadrado perfecto.
g(x) = -(x2 + 2(3)x) – 7 = -(x2 + 2(3)x + (3)2) – 7 + 9 = -(x + 3)2 + 2. De esta manera la función se reescribe como g(x) = -(x + 3)2 + 2.
Así la gráfica de la función g la obtenemos a partir de la función f(x) = x2, (1) trasladando f, 3 unidades hacia la izquierda, (x + 3)2; (2) efectuando una reflexión de f sobre el eje x, -(x + 3)2 y (3) efectuado una traslación vertical hacia arriba 2 unidades, -(x + 3)2 + 2.
|
|
|
|
f(x) = x2 |
Paso (1) |
|
|
|
|
Paso (2) |
Paso (3) |