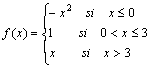Problema. 35.
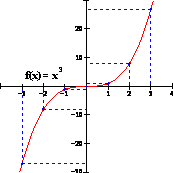
Graficar f(x) = x3
|
x |
f(x) = x3 = y |
Puntos |
|
|
-3 -2 -1 0 1 2 4 |
f(-3) = (-3)3 = -27 f(-2) = (-2)3 = -8 f(-1) = (-1)3 = -1 f(0) = (0)3 = 0 f(1) = (1)3 = 1 f(2) = (2)3 = 8 f(3) = (3)3 = 27 |
(-3, -27) (-2, -8) (-1, -1) (0, 0) (1, 1) (2, 8) (3,27) |
Problema. 36.
|
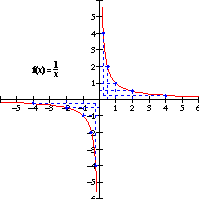
Graficar |
|||
|
x |
f(x) = 1/x = y |
Puntos |
|
|
-4 |
f(-4) = -¼ = -¼ |
(-4, -¼) |
|
|
-2 |
f(-2) = -½ = -½ |
(-2, ½) |
|
|
-1 |
f(-1) = -1/1 = -1 |
(-1, -1) |
|
|
-½ |
f(-½) =-1/(-½) = -2 |
(-½, -2) |
|
|
-¼ |
f(-¼) =-1/(-¼) = -4 |
(-¼, -4) |
|
|
½ |
f(½) =-1/(½) = 2 |
(½, -2) |
|
|
¼ |
f(¼) =1/(¼) = 4 |
(¼, 4) |
|
|
1 |
f(1) = 1/1 = 1 |
(1, 1) |
|
|
2 |
f(2) = ½ = ½ |
(2, ½) |
|
Problema. 37.
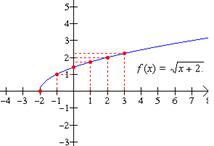
Trazar la gráfica de f (x) = 
|
Solución: Primero observamos que |
||
|
x |
|
|
|
-2 -1 0 1 2 3 |
0 1
2
|
|
Problema. 38.
Graficar la función valor absoluto 
Recordemos que el valor absoluto se define de la siguiente manera
. Por lo tanto tenemos que la función es equivalente a
.
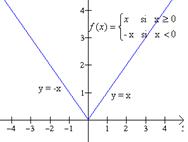
Recordemos también que una función es una regla. Para esta función en particular la regla es la siguiente: Primeramente se considera el valor de entrada x. Si x ≥ 0, entonces el valor de f (x) es x; por otra parte, si x < 0. Entonces el valor de f (x) es -x.
|
Para trazar la grafica observemos que si x ≥ 0, entonces f(x) = x, así que la parte de la gráfica de f que se encuentra a la derecha de x = 0, es la recta y = x que tiene pendiente 1 y que pasa por el origen. Si x < 0 entonces f(x) = -x, de modo que la parte de la gráfica de f que se encuentra a la izquierda de la recta x = 0 debe coincidir con la gráfica de y = -x, que es una recta con pendiente -1 y que pasa por el origen. Ver la gráfica de la derecha. |
|
Problema. 39.
|
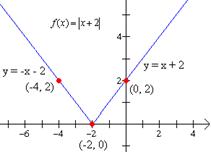
Trazar la gráfica de f(x) = |x +2| |
||||
|
Solución: Por la definición de valor absoluto sabemos que |x + 2| = x + 2 cuando x + 2 ≥ 0, es decir si x ≥ -2 y = |x + 2| = -(x + 2) = -x – 2, cuando x+2 < 0, esto es si x < -2. En otros términos esta función es equivalente a la función definida por secciones: |
x |
f(x) |
|
|
|
-4 -3 -2 -1 0 1 2 3 |
2 1 0 1 2 3 4 5 |
|||
Problema. 40.
|
Trazar la gráfica de la función definida por secciones
|
|
|
Solución: Nótese que f no representa tres funciones sino más bien, a una función cuyo dominio es el conjunto de números reales. Sin embargo, la gráfica de f consta de tres secciones obtenidas trazando, a su vez: |
|
|
y = -x2 en el intervalo x ≤ 0 y = 1 en el intervalo 0 < x ≤ 3 y y = x en el intervalo x > 3. La gráfica se muestra a la derecha. |
|
Problema. 41.
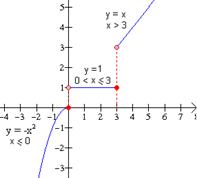
Graficar la función racional 
.
Solución: Primero obtenemos las intersecciones con los ejes coordenados. La intersección y es 
, y la intersección x se encuentra resolviendo 
, cuya solución es x = 3. De donde las intersecciones con los ejes están dadas por los puntos (0, -3) y (3, 0). Cuando se trazan gráficas de funciones racionales, es importante tomar nota del dominio; en este caso, es evidente que el dominio de f es el conjunto de todos los números reales excepto x = 1, ya que para x = 1 la función no está definida. Como se muestra en la tabla 1, cuando x está cerca de 1, los valores del denominador x-1, se encuentran muy cerca de cero y por consiguiente los valores correspondientes de f(x) son grandes en valor absoluto. Es claro que algo dramático sucede cuando x se acerca a 1. En efecto, la tabla 1 nos indica que los valores de f(x) aumentan sin límite. Hemos indicado esto dibujando una línea punteada vertical, llamada asíntota vertical, en x = 1. Cuando x se aproxima a 1, la gráfica se acerca cada vez más a esta recta, pero esta recta no es pare de la gráfica de la función, es sólo una guía. Obsérvese que la función también tiene una asíntota horizontal, concretamente la recta y = -1. Esto puede verse en la tabla 2, cuando la x toma valores positivos muy grandes (p. e. x= 300), el valor de la función f(x) se acerca a la recta y = -1, y cuando la x toma valores grandes pero negativos (p. e. x = -300), la función también se acerca a la recta y = -1.
|
Tabla 1 |
|
Tabla 2 |
|
||
|
x |
f(x) |
|
x |
f(x) |
|
|
0.60000 0.80000 0.98000 0.99333 1.00000 1.00667 1.02000 1.20000 1.40000 |
-6.00000 -11.00000 -101.00000 -301.00000 Indefinido 299.00000 99.00000 9.00000 4.00000 |
|
273.33333 280.00000 286.66667 293.33333 300.00000 -300.00000 -293.33333 -286.66667 -280.00000 |
-0.99266 -0.99283 -0.99300 -0.99316 -0.99331 -1.00664 -1.00680 -1.00695 -1.00712 |
|
