3. Graficación.
Algunas funciones que se hallan frecuentemente en el Cálculo se enumeran a continuación:
|
Función Constante: |
f(x) = b |
|
Función lineal: |
f(x) = mx +b |
|
Función cuadrática: |
f(x)=ax2 + bx + c (a ≠ 0) |
|
Función polinómica de grado n: |
f(x) = anxn+an-1xn-1+…+a0 (n = entero no negativo; an≠0) |
|
Función Racional: |
f(x) = g(x)/(x) donde g(x) y h(x) son polinomios y h(x) ≠ 0 |
|
Función Potencia: |
F(x) = axn (n= cualquier número real) |
A. Información acerca de las rectas.
La pendiente de una recta que pasa a través de los puntos (x1, y1), y (x2, y2) (donde x1≠ x2) es ![]() .
.
Dos rectas son perpendiculares cuando el producto de sus pendientes es -1. Si una recta L1 tiene pendiente m1 = 2 y es perpendicular a la recta L2, entonces m1m2 = -1. De donde la pendiente de la recta L2 es m2 = -1/2.
La ecuación de recta que pasa a través de (x1, y1) con pendiente m es: ![]()
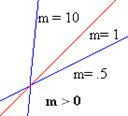
La ecuación de la recta con pendiente m e intersección y en b es: y = mx + b. La pendiente m nos indica hacia donde y que tanto se inclina la recta.
|
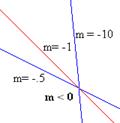
Si m > 0, la recta se inclina hacia la derecha. Si m < 0, la recta se inclina hacia la izquierda. Si m = 0, la recta es horizontal. |
|
|
|
Problema. 25.
Graficar la función lineal ![]() .
.
|
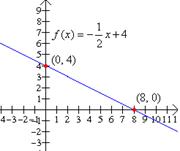
Solución: para graficar una función lineal se necesita encontrar dos puntos que satisfagan la ecuación y unirlos con una línea recta. Como la gráfica de una función lineal es una línea recta, todos los puntos que satisfacen la ecuación deben estar en la línea. Los dos puntos que encontraremos serán las intersecciones de la línea recta con los ejes coordenados x e y. La intersección x es el punto donde la grafica cruza el eje x; la intersección y es donde la recta cruza el eje y. Como la recta cruza el eje y donde x = 0, la coordenada x de la intersección y es siempre 0. La coordenada y de la intersección y se obtiene, entonces, simplemente igualando x a cero y resolviendo la ecuación para y.
|
|
|
Para hallar la intersección con el eje x, hacemos y = 0 y resolvemos para x:
|
|
|
Entonces graficando los puntos (0, 4) y (8, 0) y uniéndolos con una línea recta, tenemos la gráfica de arriba. La pendiente de esta recta es m = -1/2. |
|
Problema. 26.
|
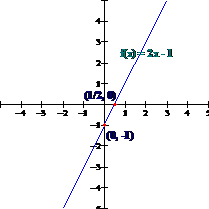
Trazar la gráfica de la función f (x) = 2 x – 1. Solución: Una forma de encontrar la grafica de una ecuación lineal es encontrar dos puntos por los cuales pasa la recta. Si estos puntos son las intersecciones con los ejes coordenados, tendremos bien ubicada la posición de la recta. Para encontrar la intersección con el eje y evaluamos la función en x = 0 y obtenemos f(0) = 2(0) – 1 = -1. Para encontrar la intersección con el eje y, hacemos y = 0, es decir 0 = 2x – 1. Despejamos la variable x obtenemos x = ½. |
|
|
En conclusión, obtenemos que las intercepciones con los ejes están dadas por los puntos (0, -1) y (½., 0). La pendiente de esta recta es m = 2. |
|
Problema. 27.
|
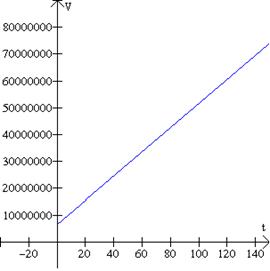
Las ventas de una fabrica de productos químicos local crecieron de $6 500 000 en 1980 a $ 11 000 000 en 1990. Suponiendo que las ventas se aproximan a una función lineal (V(t) = mt + b), exprese las ventas S como una función de tiempo t. Solución: Haciendo 0 = 1980 y 10 = 1990 se tiene que la pendiente de la recta es:
Sustituyendo por V = 6500000 en t = 0 650000 = m(0) + b, se obtiene b = 6500000. De donde la función es: V(t) = 450000t + 500000. |
|
Problema. 28.
|
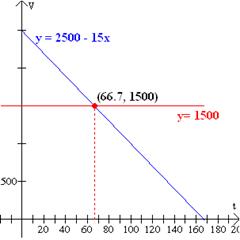
Una nutricionista desea mezclar granos de $10.00 el kilo, con otros de $25, con el, fin de obtener 100 kilos de una mezcla de $ 15 el kilo. ¿Cuánto de cada uno de los granos debe ir en la mezcla? Solución: Sea x = la cantidad de granos de $ 10.00; entonces (100 – x) será la cantidad de granos de $ 25.00 y m(x) = 10x + 25 (100 – x) = 2500 – 15x Sustituyendo el valor de la mezcla deseada para m, 15(100) = 2500 – 15x 15x = 2500-1500 = 1000 |
|
|
x = 1000/15 = 66.7 kilos de $10.00 100-x =100 – 66.7 = 33.3 kilos de $25.00 |
|
Problema. 29.
|
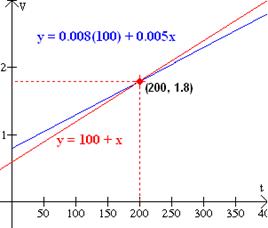
¿Qué cantidad de aceite con contenido de 0.5% de azufre debe mezclar un químico, en 100 litros con 0.8% de azufre para conseguir un aceite que contenga 0.6% Solución: Haciendo x = la cantidad de aceite de 0.5% para mezclar, tenemos m(x) = 0.008(100) + 0.005x Luego, sustituyendo la mezcla deseada de (100 + x) litros de 0.6% de azufre para m, 0.006(100 + x) = .008(100) + .005x 0.6 + .006x = 0.8 + .005x 0.001x = 0.2 x = 200 |
|