11. Problemas para resolver

I.         Para cada una de las funciones, calcule los valores indicados.

1.  f(x) = 3x² + 5x – 2;             f(1),  f(0),  f(-2),  f(a + h)

2.                                    g(2), g(0), g(-1), g(a – h)

3.           h(3), h(1),  h(0),  h(-3)
 

II.        Especifique el dominio, el rango  y la gráfica de las siguientes funciones.

1.                    3.  h(x) = 3x² – 6                     5.  J(x) = x³ – 2x + x²

2.                       4.                         6.  
 

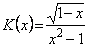
III.      Determine si las siguientes funciones son pares,  impares o ninguno de los casos.

1.  f(x) = 2x³ – 4x                    3.  
 

2.                        4.  I(x) = x² + 2x  + 2

IV.       Graficación con transformaciones.

1. Represente gráficamente la función f(x) = x². Luego, sin cálculos adicionales, represente gráficamente.

     (a)   f(x) = -x²                     (b)  f(x) = x² + 3                      (c)  f(x) = 4 – (x+1)²

2.  Represente gráficamente la función . Luego, sin cálculos adicionales,  represente gráficamente.

                (a)          (b)        (c)  

3.  Represente gráficamente la función . Luego, sin cálculos adicionales represente gráficamente.

                (a)                   (b)                    (c)  

V.      En los problemas 1 – 3 encuentre f + g,   f – g,   f × g,   f / g,   f×(g-f),   g.(g/f) y especifique su dominio:

1.  f/x) = 3x²,                           

2.  f(x) = x³ + 3x,                     

3.  ,                  g(x) = 2x + 1

VI.    Dadas f y g funciones, encuentre (f o g)(x) y (g o f)(x)

            1.  f(x) = x³ ,                            g(x) = x + 1

            2.   ,                g(x) = 7x² + 1

            3.  f(x) = x³ – 1  ,                     

VII.   Para  cada una de las siguientes funciones investigue si son uno a uno. En tal caso, encuentre su inversa y verifique que lo son

            1.                       3.  h(x) = x³ – 2

            2.                         4.  I(x) = (x – 1) (x + 1)

VIII. En los siguientes problemas trace la gráfica de la función dada. Además determine la amplitud, el período y el desplazamiento de fase.

            1)   y = 1 + sen(x)               2)   y = 1 + sen(x)               3)  y = 2 – sen(x)

            4)   y = 2 + cos(x)               5)   y = 3cos(2p + x)         6)  

            7)   y = 2tan(x + p)             8)   y = 4 – 3tan(2p -x)     9)   y = 2 + tan(x)

          10)  y = cot(3x)                   11)  y = 2cot(x +p)           12)  y = -3cot(x)

          13)  y = sec(x + p)              14)  y = -3sec(2x)             15)  y = 2 + sec(x)

IX.    Resuelva los siguientes problemas.

1.      La densidad (p) del dióxido de carbono varía con su calor específico a volumen constante (Cv) según la ecuación:
                    Cv = 0.691 + 0.889p + 1.42p²
Construir la gráfica de esta ecuación para los valores de p entre 0.1 y 0.4 gml^-1 y así hallar la densidad cuando Cv = 0.88jg^{-1 C.}

2.      El incremento del calor emitido (DH) para la reacción
                    N₂(g) + 3H₂(g) = 2NH₃(g)
a la temperatura T, en grados Kelvin, está dado por
                   DH = 3.4 x 10 ^–6 T³ – 1.15 x 10^-3T² – 9.92 T – 19000
Construir una gráfica  DH en función de T, para valores de T comprendidos entre T = 300⁰K y T = 1400⁰K. De aquí hallar DH cuando T = 980⁰K, DH está en calorías.

3.      La relación entre la presión (p) y el volumen (v) de un gas perfecto está dado por la expresión
                          pv = 24.6
            Donde p se mide en atmósferas y v en litros. Hacer una gráfica de v en función de p, para los valores de p comprendidas entre 0.1 y 10 atm. Hallar el volumen del gas cuando p = 0 y p = 1.3.