A. Una forma distinta para graficar funciones senos y cosenos
El siguiente ejemplo ilustra una forma para graficar las funciones f(x) = a sen b(x +c) + d, y g(x) = a cos b(x + c) + d.
Problema. 95.
Graficar f(x) = 2 sen (4x + p) -1.
Solución: Observe que el valor de b, representado aquí por 4, es positivo. Si b < 0, el método se puede utilizar después de aplicar las propiedades de las funciones trigonométricas correspondientes.
Para bosquejar un período de la gráfica de la función, se seguirán los siguientes pasos.
Paso 1. Determine un intervalo cuya longitud es un período de la función, resolviendo la desigualdad siguiente:
0 £ 4x + p £ 2p
Este método funciona porque todos los valores de las funciones seno y coseno se encuentran en el intervalo [0, 2p]. La solución de la desigualdad es
![]()
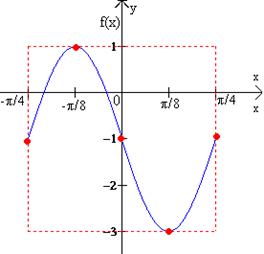
El período de la función es la longitud de este intervalo, -p/4 – (-p/4) = p/2. El desplazamiento de fase es -p/4, el valor izquierdo del intervalo.
|
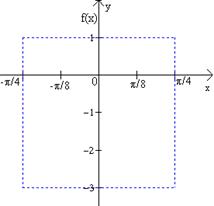
Paso 2. Determine el rango de f reemplazando sen (4x + p) en la función por sus valores mínimo, y máximo, -1, y 1, respectivamente, es decir: 2(-1) -1 = -2 – 1 = -3; y 2(1) – 1 = 2 – 1 = 1. Así pues encontramos que el rango, es el intervalo, [-3, 1]. La amplitud de la gráfica es la mitad de la diferencia de los valores máximo y mínimo de la función, que en este ejemplo es [1 – (-3)]/2 = 2 Paso 3. En un sistema de coordenadas, bosqueje con líneas punteadas el rectángulo formado por las rectas x = -p/4 y x = p/4 (son los extremos del |
|
|
intervalo que se obtuvo en el paso 1) y las rectas horizontales y = -3 y, y = 1 (son los extremos del intervalo del rango que se obtuvo en el paso 2.) |
|
|
Paso 4. Divida el intervalo que se obtuvo en el paso 1 en cuatro partes. Al dividir el intervalo en cuatro obtenemos los siguientes valores, -p/4, -p/8, 0, p/8, y p/4. Luego evaluamos la función en estos cinco valores como se muestra en a tabla. |
||
|
Paso 5. Dibuje los cinco puntos obtenidos en el paso 4 y únalos con una curva suave, como se muestra en la gráfica |
||
|
|
|
|
|
x |
f(x)=2sen(4x+p)-1 |
|
|
|
2sen(0)–1=2(0)–1=-1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Problema. 96.
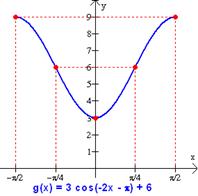
Graficar la función g(x) = 3 cos(-2x - p) + 6
Solución: Primero reescribimos la función aplicando la identidad cos (-u) = cos u.
g(x) = 3 cos [- (2x + p)] + 6 = 3 cos (2x + p) + 6.
Después le aplicamos el método anterior.
|
Paso1. Determine un intervalo cuya longitud es un período de la función, resolviendo la desigualdad siguiente; 0 £ 2x + p) £ 2p, cuya solución es -p/2 £ x £ p/2. El período de la función es (p/2)-(- p/2) = p. Paso 2. Determinamos el rango. (a) 3(1) + 6 = 9; (b) 3(-1) + 6 = 3. Así el rango es el intervalo [9, 3]. La amplitud de la función es 9 – 3 = 6. Paso 3. Bosquejamos un rectángulo formado por los intervalos -p/2 £ x £ p/2, y [3, 9]. |
|
Paso 4. Dividimos el intervalo -p/2 £ x £ p/2, 1 en cuatro partes. Al dividir el intervalo en cuatro obtenemos los siguientes valores, -p/2, -p/4, 0, p/4, y p/2. Luego evaluamos la función en estos cinco valores como se muestra en a tabla.
|
Paso 5. Dibuje los cinco puntos obtenidos en el paso 4 y únalos con una curva suave, como se muestra en la gráfica |
|
|
|
x |
g(x) = 3 cos(2x + p) + 6 |
|
|
-p/2 |
g(-p/2)=3cos(0)+6=3(1)+6=9 |
|
|
-p/4 |
g(-p/4)=3cos(p/2)+6=3(0)+6=6 |
|
|
0 |
g(0)=3cos(p)+6=3(-1)+6=3 |
|
|
p/4 |
g(p/4)=3cos(3p/2)+6=3(0)+6=6 |
|
|
p/2 |
g(p/2)=3cos(2p)+6=3(1)+6=9 |
|
|
|
|
|
Problema. 97.
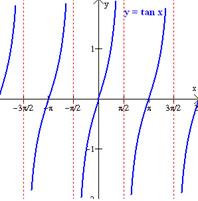
Graficar f(x) =tan x.
|
Solución: La tangente se puede definir de la siguiente manera |
x |
tanx |
|
0 |
0 |
|
|
±p/6 |
± |
|
|
±p/4 |
±1 |
|
|
±p/3 |
± |
Analicemos la tangente en el intervalo -p/2 < x < p/2.
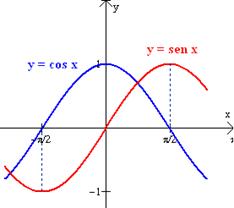
Si x está cerca de -p/2, entonces la tangente es negativa y muy grande, puesto que cos x está cerca de cero y sen x está cerca de -1. Si x está cerca de p/2, entonces la tangente es positiva y muy grande, ya que cos x está muy cerca de cero y sen x muy cerca de 1. Observa la figura donde estan las funciones seno y coseno.
La gráfica de la función tan x, es una función de período p y se muestra abajo.
|
|
|
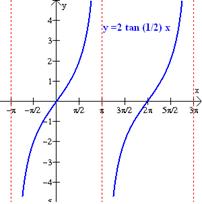
Problema. 98. Graficar la función t(x) = 2 tan yx.
|
Solución: No hay una amplitud definida para la curva de la tangente pero el efecto de la multiplicación por el 2, es el de alargar la curva. Puesto que el período fundamental de la función tangente básica es p, el periodo de esta curva es p/(1/2) = 2p. La gráfica se muestra a la derecha. |
|