10. Funciones Trigonométricas.
Problema. 88.
Analizar la función f(x) = a sen b(x- h) + c
Solución:
|
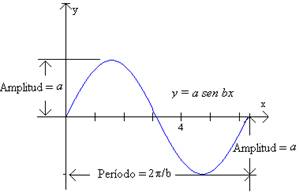
Consideremos primero la gráfica de f(x) = a sen bx, donde a y b son constantes positivas. El factor a causa una expansión o contracción vertical de la gráfica, dependiendo de si a > 1 o 0 < b < 1. En particular, cuando la curva seno básica tiene su altura máxima 1, la nueva curva alcaza la altura a. El factor b causa una expansión horizontal si 0 < b < 1 y una contracción si b > 1. |
|
Por periodicidad entendemos que sen (bx +2p) = sen bx. Si reescribimos la parte izquierda de esta ecuación como sen b(x +2p/b). Tenemos
![]()
Así, la gráfica de y = a sen bx se repite cada 2p/b unidades. Esto es, el período es 2p/b. La figura ilustra una gráfica típica de la forma y = a sen bx.
Si en la ecuación y = a sen bx el número a es negativo, entonces la gráfica se refleja sobre el eje x. Si b < 0, utilizamos el hecho de que sen bx = -sen(- bx), así que de nuevo tenemos una reflexión. Por ejemplo, la gráfica de y = 2sen (-3x) es la misma que la de y = -2sen3x, que es la reflexión de y = 2sen 3x. Por supuesto, si a < 0 y b < 0, no hay una reflexión, y por tanto no hay un cambio neto.
|
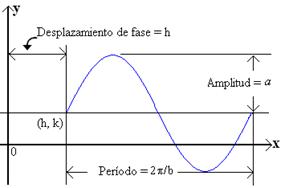
Si reemplazamos x por x – h y, y por y – k, entonces obtenemos una traslación de la grafica h unidades horizontalmente y k unidades verticalmente. La gráfica de y – k = a sen b(x – h). o equivalentemente, y = a sen b(x – h) + k. la figura que se muestra es para los valores de a > 0 y b > 0. El valor h se conoce como el desplazamiento de fase. |
|
Problema. 89.
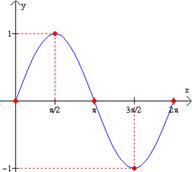
Graficar f(x) = sen x.
|
Solución: Consideremos la función en el intervalo 0£ x £ 2p. Su amplitud es 1 y su periodo es 2p. La tabla de la izquierda muestra los valores interesantes de la gráfica. |
x |
y |
|
|
0 |
0 |
||
|
p/2 |
1 |
||
|
p |
0 |
||
|
3p/2 |
-1 |
||
|
2p |
0 |
||
|
|
|
|
Problema. 90.
|
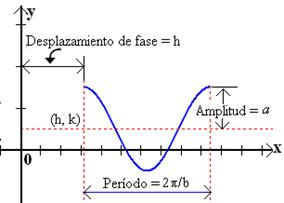
Analizar la función g(x) = acosb(x – h)+c Solución: Un análisis similar puede hacerse para la función coseno, una grafica usual de la ecuación de la forma y = a cos b(x – h) se muestra en la figura adjunta. Puesto que la función coseno es una función par, entonces cos(-bx) = cos bx, así si b es negativo, la gráfica no se afecta. |
|
Problema. 91.
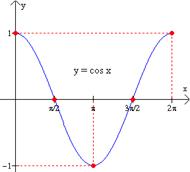
Graficar la función g(x) = cos x.
|
Solución: Consideremos la función en el intervalo 0£ x £ 2p. Su amplitud es 1 y su periodo es 2p. La tabla de la derecha muestra los valores interesantes de la gráfica. |
x |
y |
|
|
0 |
0 |
||
|
p/2 |
1 |
||
|
p |
0 |
||
|
3p/2 |
-1 |
||
|
2p |
0 |
Problema. 92.
Bosqueje la gráfica de f(x) = 3 sen (½)x
Solución: La amplitud es 3 y el período es 2p/(½) = 4p. La gráfica se muestra en la figura.
Problema. 93.
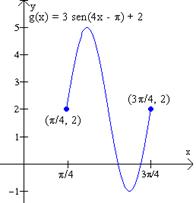
Bosqueje la gráfica de la función g(x) = 3 sen(4x - p) + 2.
Solución: Primero reescribimos la función para identificar los datos importantes de la gráfica, para ello factorizamos el 4 para reescribir la función en la forma siguiente:
![]()
Esta es una función seno con amplitud 3, y período p = 2p/4 = p/2, y desplazamiento de fase p/4 unidades hacia la derecha, y trasladada verticalmente 2 unidades hacia arriba.
|
|
|
Problema. 94.
|
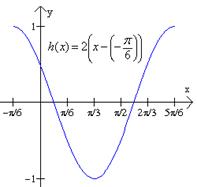
Graficar la función h(x) = cos(2x + p/3). Solución: Primero escribimos la ecuación en la forma
En esta ecuación identificamos que el desplazamiento de fase es -p/6. Esto indica que la curva se desplazó p/6 unidades a la izquierda. La amplitud es 1, y el período es 2p/2 = p. |
|