Funciones Logarítmicas.
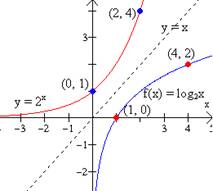
Intercambiando las variables de una función exponencial f definida por y = bx, es posible obtener una nueva función g definida por x = ay tal que cualquier par ordenado de números en f también se hallen en g, en orden invertido. Por ejemplo, si f(2) = 4, entonces, g(4) = 2; si f(3) = 8, entonces g(8) = 3, como se ve en la figura de abajo. La nueva función g, la inversa de la función exponencial f, se denomina una función logarítmica con base b. En lugar de x = by, la función logarítmica con base b se expresa más comúnmente
y = logbx b > 0, b ≠ 1.
Expresar un logaritmo con base b de número x es el exponente al que debe de elevarse para obtener x.
Características de las funciones y = logbx
1. El dominio de la función es el conjunto de todos los números reales positivos; el rango es el conjunto de todos los números reales.
2. Para la base b > 1, f(x) es creciente y cóncava hacia abajo. Para 0 < b < 1, f(x) es decreciente y cóncava hacia arriba.
Problema. 85.
Graficar f(x) = log2x.
Solución: primero escribimos la función como y = log2x, después expresamos la función en forma exponencial x = 2y. Después hacemos dos tablas de datos, una con valores para la función x = 2y,y otra con los valores de y y x invertidos, que serán los de la función exponencial.
|
x |
2y |
|
x |
log2x |
|
|
0 |
1 |
|
1 |
0 |
|
|
1 |
2 |
|
2 |
1 |
|
|
2 |
4 |
|
4 |
2 |
|
|
3 |
8 |
|
8 |
3 |
|
|
4 |
16 |
|
16 |
4 |
|
|
-1 |
-½ |
|
-½ |
-1 |
|
|
-2 |
-¼ |
|
-¼ |
-2 |
|
|
-3 |
-⅛ |
|
-⅛ |
-3 |
|
|
-4 |
- |
|
- |
-4 |
|
|
Observa que las funciones y = 2x y, y = log2x, son inversas una |
|||||
Problema. 86.
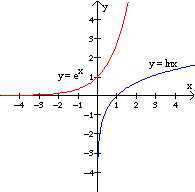
Trazar la gráfica de la función f(x) = ln(x).
Solución: La inversa de la función ln(x) es la función exponencial y = ex, para graficar y = ln(x), hacemos una tabla de la función y = ex y después invertimos los datos de la tabla para graficar y = ln(x).
|
x |
y = ex |
|
x |
y = lnx |
|
|
0 |
1 |
|
1 |
0 |
|
|
1 |
2.71 |
|
2.71 |
1 |
|
|
2 |
7.38 |
|
7.38 |
2 |
|
|
3 |
20.08 |
|
20.08 |
3 |
|
|
4 |
54.59 |
|
54.59 |
4 |
|
|
-1 |
0.36 |
|
0.36 |
-1 |
|
|
-2 |
0.13 |
|
0.13 |
-2 |
|
|
-3 |
0.04 |
|
0.04 |
-3 |
|
|
-4 |
0.01 |
|
0.01 |
-4 |
Problema. 87.
|
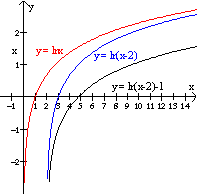
Trazar la grafica de la función g(x) = ln(x – 2) – 1. Utilizando transformaciones. Solución: Se empieza con la gráfica de y = ln(x) anterior, y usando la transformaciones, (1) se traslada dicha gráfica dos unidades a la derecha para obtener la gráfica de y = ln(x – 2) y luego (2) se traslada ésta una unidad hacia abajo para obtener la gráfica de y = ln(x – 2) – 1. |
|