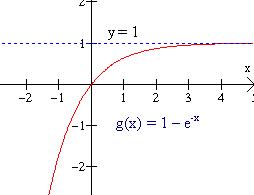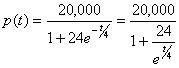9. Funciones Exponenciales y Logarítmicas.
La función definida por: f(x) = bx donde b > 0, b ≠ 1, yel exponente x es un número real, se llama una función exponencial con base b.
1. El dominio de una función exponencial son todos los reales
2. El rango son todos los números positivos.
3. Puesto que b0 = 1 para toda base b, cada gráfica tiene la intersección-y, (0, 1), no intercepta el eje x.
4. Si b > 1, la gráfica de y = bx crece de izquierda a derecha. Esto es, cuando x aumenta su valor, y también aumenta su valor.
5. 0 < b < 1, entonces la gráfica de y = bx decrece de izquierda a derecha. Es decir, cuando x aumenta su valor, entonces y disminuye su valor.
Problema. 76.
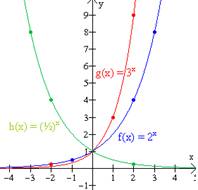
Graficar las funciones exponenciales f(x) = 2x, g(x) = 3x , h(x) = (½)x.
Solución: Evaluamos las funciones en varios valores de x reales y los mostramos en la tabla de datos.
|
x |
2x |
3x |
(½)x |
|
|
-2 |
¼ |
|
4 |
|
|
-1 |
½ |
|
2 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
2 |
3 |
½ |
|
|
2 |
4 |
9 |
¼ |
|
|
3 |
8 |
27 |
|
|
|
|
||||
Problema. 77.
|
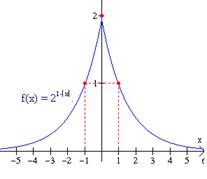
Graficar la función definida por: f(x) 21-çxç Solución: Primero hacemos una tabla de datos. |
|
|||
|
x |
f(x) |
x |
f(x) |
|
|
0 |
2 |
0 |
2 |
|
|
1 |
1 |
-1 |
1 |
|
|
2 |
½ |
-2 |
½ |
|
|
3 |
½ |
-3 |
½ |
|
|
4 |
⅛ |
-4 |
⅛ |
|
|
Observa que la función es par. También observa que cuando x aumenta en valor absoluto, y se aproxima acero. Así que el eje x es una asíntota horizontal. La gráfica se muestra a la derecha. |
||||
Problema. 78.
Un cultivo de bacterias, con un número inicial de 1000 bacterias, dobla su tamaño cada hora. Encuentra una fórmula para el número N(t) de bacterias presentes después de t horas. Cuantas bacterias estarán presentes después de 8 horas.
Solución: después de una hora se tiene
N(1) = 1000(2)
bacterias presentes. Después de 2 horas este número se dobla, dando,
N(2) = 1000(2)(2) = 1000(22)
Después de 3 horas, se dobla de nuevo, dando,
N(3) = 1000(23)
Continuando de esta manera, obtenemos la fórmula
N(t) = 1000(2t)
Así que después de 8 horas, la cantidad de bacterias es
N(8) = 1000(28) = 256,000.
Problema. 79.
Supongamos que una cantidad de azúcar se coloca en agua, y que el 10% se disuelve cada minuto. Sea Q(t) la cantidad de azúcar presente después de t minutos. Si inicialmente hay 5 kilos de azúcar, es decir, Q(0) = 5, encuentre aproximadamente cuanta azúcar estará presente después de 15 minutos.
Solución: cada minuto se disuelve el 10% de azúcar, así que el 90% permanece sin disolver. Así después de un minuto la cantidad presente de azúcar es
Q(1) = 5(0.9)
Y después de 2 minutos, el 90% de Q(1) es
Q(2) = 5(0.9)(0.9) = 5(0.9)2
Continuando de esta manera, obtenemos
Q(t) = 5(0.9)t
Así,
Q(15) = 5(0.9)15 » 1.03 kilos.
Problema. 80.
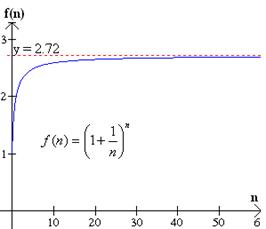
Entre todas las posibles bases de las funciones exponenciales, sin duda destaca una que es muy importante en las matemáticas y en las aplicaciones a fenómenos del mundo real. Este es un número irracional que está designado por la letra e y su valor es aproximadamente 2.71828. La siguiente es una forma de definir el número e. Consideremos la expresión
![]()
Donde n designa a cualquier número entero positivo. Evaluamos esta expresión para algunos valores de n en la tabla de abajo. Esto debe de convencernos (aunque esto no es prueba) de que cuando n se hace cada vez más grande [1 + / (1/n)] se aproxima cada vez más a un número cuyos primeros dígitos son 7.718.
|
n |
f(n) |
|
|
1 |
2 |
|
|
2 |
2.25 |
|
|
3 |
2.3707 |
|
|
4 |
2.44141 |
|
|
5 |
2.48832 |
|
|
10 |
2.59374 |
|
|
100 |
2.70481 |
|
|
1,000 |
2.71692 |
|
|
10,000 |
2.71815 |
|
|
1,000,000 |
2.71828 |
|
|
Decimos que el límite de [1+(1/n)] cuando n tiende al infinito es e y escribimos |
||
Problema. 81.
|
Graficar la función g(x) = 1 – e-x . |
|
|
Solución: La curva es asintótica, hacia la derecha, a la recta y = 1, ya que cuando x crece indefinidamente, e-x = 1/ex se aproxima a cero, así que 1 – e-x se aproxima a 1. También se puede graficar como una sucesión de transformaciones de la función f(x) = ex. (1) f(-x) = e-x, una reflexión sobre el eje y; (2) –f(-x) = -e-x, una reflexión sobre el eje x; (3) –f(-x) + 1 = -e-x + 1 = 1 – e-x = g(x), una traslación vertical hacia arriba. |
Problema. 82.
La población proyectada P de una ciudad esta dada por
P = 100,000e0.05t,
Donde t es el número de años después de 1990. Predecir la población para el año 2010.
Solución: El número de años desde 1990 a 2010 es 20, así que t = 20. Entonces
P = 100,000e0.05(20) = 100,000e1 = 100,000e
Puesto que e » 2.1828,
P » 100,000(2.71828) = 271.828.
Muchas predicciones se basan en estudios de población.
Problema. 83.
Un elemento radioactivo decae de tal manera que después de t días el número de N miligramos presentes, está dado por
N = 100e-0.062t,
(a) ¿Cuantos miligramos están presentes inicialmente?
(b) ¿Cuántos miligramos están presentes después de 10 días?
Solución: (a) Para calcular la cantidad inicial debemos de considerar el tiempo igual a cero, es decir, calcular N cuando t = 0. Así, si t = 0, entonces N(0) = 100e-0.062(0) =100 miligramos están inicialmente presentes.
(b) Cuando t = 10,
N = 100e-0.062(10) = 100e-0.62
» 100(0.53794) » 53.8
Problema. 84.
|
Hay un límite máximo sobre la población de peces en un cierto lago debido a la cantidad de oxigeno, alimentación, etc. proporcionadas. La población de peces en este lago en el tiempo t, en meses está dado por la función
¿Cuál es el límite máximo de la población de peces? |
|
|
Solución: La gráfica de p(t) nos sugiere que la línea horizontal y = 20,000 es una asíntota de la gráfica. En otras palabras, la población de peces nunca crecerá arriba de 20,000. Esto se puede confirmar algebraicamente reescribiendo la regla de p en la siguiente forma:
Cuando t es muy grande, entonces t/4 también lo es. Por lo tanto |
|