Sea f una función y c un número real, entonces la gráfica de la función definida por f(cx) es:

1. Una contracción horizontal si | c | > 1

2. Una expansión horizontal si | c | < 1

3. Si c es negativo, además de la contracción o expansión se obtiene una reflexión sobre el eje y.

Ejemplo 2.9.

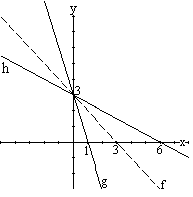
 Sea f la función definida por f(x) = 3-x. La gráfica de f es una línea recta que corta los ejes en los puntos (0,3) y (3,0)

a). Si substituimos x por 3x en la función f obtenemos la función g(x) = 3 – 3x, cuya gráfica es una contracción horizontal de la función f(x) = 3 – x. Obsérvense que cada punto (m, n) de la gráfica de f se transforma en un punto de la forma (m/c, n) de g; por ejemplo el punto (3,0) de f se convierte en el punto (1,0) de g.

b) Si en f(x) = 3-x reemplazamos x por ½ x se obtiene la función h(x) = 3-x/2, cuya gráfica es una expansión horizontal de la función f(x) = 3-x.

Ejemplo 2.10

 Si g(x) = , entonces la gráfica de g(-x) =  es la gráfica de g reflejada sobre el eje y.

Ejemplo 2.11

Grafique la función h(x)=-2x² +12x -17

Solución:

Completando el “Trinomio cuadrado”, f(x) se transforma en h(x) =-2(x-3)² +1.

Obsérvese que la gráfica de f es la misma que la de la función g(x)=x² bajo las siguientes transformaciones.

i)     Una translación horizontal de 3 unidades hacia la derecha de g(x) = x²; esto es g₁(-3) = (x-3)²

ii)   Una expansión vertical de 2 unidades de g₁(x) = (x-3)²; es decir g₂(x) = 3(x-3)²

iii)Una reflexión sobre el eje x de g₂(x) = 2(x-3)²; o sea g₃(x) = -2(x-3)²

iv) Una translación vertical de 1 unidad hacia arriba de f(x) = -2(x-3); finalmente h(x) = -2(x-3)² + 1.