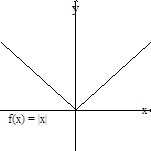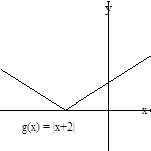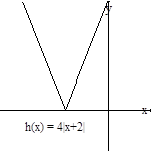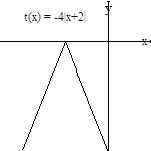Ejemplo 2.7
a) La gráfica de ![]() es una
semicircunferencia de centro (0,0) y radio 4. Si multiplicamos
f por 2 se obtiene la función
es una
semicircunferencia de centro (0,0) y radio 4. Si multiplicamos
f por 2 se obtiene la función ![]() cuya
gráfica es una expansión vertical de f(x).
cuya
gráfica es una expansión vertical de f(x).
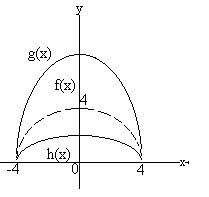
b) Si multiplicamos f por ![]() se obtiene
la función
se obtiene
la función ![]() cuya gráfica es una contracción vertical
de f(x). Las gráficas de f, g y h se muestran en el mismo sistema
de coordenadas.
cuya gráfica es una contracción vertical
de f(x). Las gráficas de f, g y h se muestran en el mismo sistema
de coordenadas.