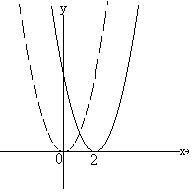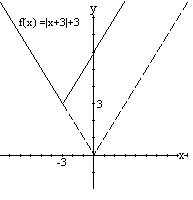2.1. Translaciones Horizontales.
Si en una función f(x) la variable x se sustituye por x – c, el efecto sobre la gráfica de f(x) es trasladar la curva una distancia c paralelamente al eje x, y en la dirección positiva, porque si (m, n) son las coordenadas de un punto sobre la gráfica de y = f(x), entonces el punto (m + c, n), que resulta de trasladar (m, n,) una distancia c en la dirección de las x positivas, caerá sobre la gráfica de y = f(x – c).
Traslación horizontal
Sea f una función y c un número real, entonces la función fc definida por f(x-c) representa una translación horizontal. La gráfica de fc es la gráfica de f trasladada |c| unidades a la derecha si c > 0 y a la izquierda si c < 0
Los siguientes ejemplos tienen como objetivo el ilustrar el principio anteriormente establecido.
|
Ejemplo 2.5
Dibuje la gráfica de f(x) = (x – 2)2
Solución.
De acuerdo con el principio recién establecido, puede obtenerse la gráfica de f(x) = (x-2)2 trasladando f(x) = x2 una distancia de |2| unidades hacia la derecha.
Esta translación se logra reemplazando x – 2 por x en f(x) = x2.
|
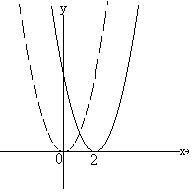
|
Ejemplo 2.6
Sea f(x) = |x|. Encuentre la función cuya gráfica se obtiene efectuando las siguientes transformaciones a la gráfica de f: una translación horizontal de 3 unidades hacia la izquierda y una translación vertical hacia arriba de 3 unidades.
|
Solución:
Para trasladar f horizontalmente 3 unidades hacia la izquierda reemplazamos en f(x) = |x| x por x + 3 y obtenemos f(x) = |x + 3|. Para efectuar la traslación vertical 3 unidades hacia arriba sumamos 3 a la última ecuación. Por lo tanto la función pedida es f(x) = |x + 3| + 3 y su gráfica es la figura mostrada.
|
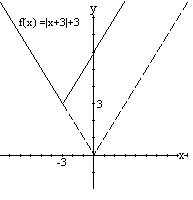
|