Ejemplo 2.1
Dibuje la gráfica de f(x) = x2 – 1
Solución.
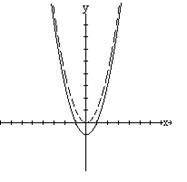
La gráfica de f(x) = x2 – 1 tiene la misma forma de la gráfica f(x) = x2 (línea punteada) sólo que ésta gráfica fue trasladada 1 unidad hacia abajo.
|
Introducción al Cálculo Diferencial e Integral
Funciones
En vista de que el comportamiento de una función puede, en general, apreciarse muy bien en su gráfica, vamos a describir algunas técnicas con ayuda de las cuales podremos hacer un trazo rápido de las curvas pero sin recurrir (todavía) a los métodos del cálculo.
Con frecuencia la gráfica de dos funciones tienen la misma forma y orientación, la única diferencia entre ellas es que una de las dos es un desplazamiento paralelo de la otra. Cualquier desplazamiento paralelo de una gráfica a otra se llama una transformación. En esta sección discutiremos la forma en que tales transformaciones ocurren. Iniciamos con las traslaciones verticales:
Sea f una función y c un número real, la suma de f + c es la función definida por f(x)+c. La gráfica de f + c es la gráfica de f trasladada |c| unidades – hacia arriba si c > 0 y hacia abajo si c < 0.
Los siguientes ejemplos tienen como propósito el ilustrar las translaciones verticales de una función.
Ejemplo 2.1 Dibuje la gráfica de f(x) = x2 – 1 Solución. La gráfica de f(x) = x2 – 1 tiene la misma forma de la gráfica f(x) = x2 (línea punteada) sólo que ésta gráfica fue trasladada 1 unidad hacia abajo. |
 |
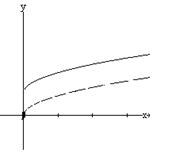
Ejemplo 2.2 Dibuje la gráfica de Solución. La
gráfica de |
 |
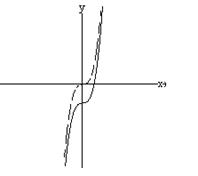
Ejemplo 2.3 Dibuje la gráfica de f(x) = x3 –2. Solución. La gráfica de f(x) = x3 – 2 es la gráfica de f(x)= x3 trasladada |-2| unidades hacia abajo. |
 |
Ejemplo 2.4 Dibuje la gráfica de Solución. La gráfica de |
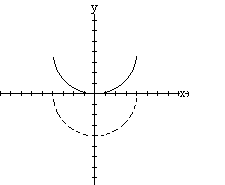 |