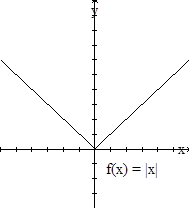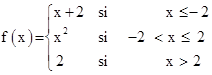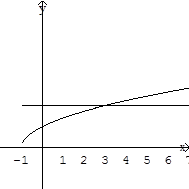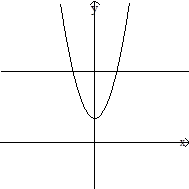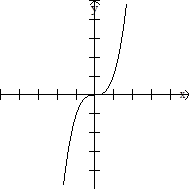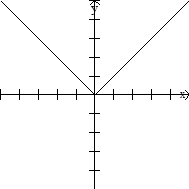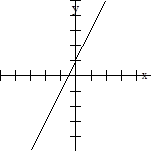1.2. La Notación Funcional.
Con frecuencia es necesario representar las
funciones por medio de símbolo de tal modo que cuado ésta es nombrada
sabemos a que función nos referimos. El símbolo más usual para
representar una función es la letra f, y el símbolo f(x) se usa
para representar el elemento asociado a x que se lee “f de x”;
algunas veces se dice que f(x) es el valor de f en x. Gráficamente, |
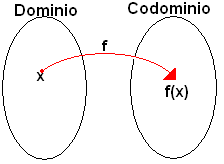
|
No deben confundirse los símbolos f y f(x); f representa la función
no está ni en el dominio x ni en el rango y. Sin embargo f(x) es un elemento
de y.
Ejemplo
1.6. Objetivo. Mostrar el uso de la notación
funcional:
Sea f la función definida por f(x) = 3x – 1. ¿Qué significa f (1)?
Solución.
f(1)
significa usar la función f para encontrar la imagen de x =1 bajo la función
f.
en |
f(x) |
= |
3x |
-1 |
reemplazar x por
1 |
|
f(1) |
= |
3(1) |
-1 |
|
|
f(1) |
= |
3 |
-1 |
|
|
f(1) |
= |
2 |
|
|
También “f(1) = 2” es una manera breve y precisa de decir “el valor
de la función cuando x = 1 es 2”.
Nótese en lo anterior que el símbolo “f(x)” únicamente reemplaza al
símbolo “y” en la ecuación y = 3x – 1.
Ejemplo 1.7.
Objetivo. Utilizar la notación f para determinar ciertos valores funcionales:
Dada la función f definida por f(x) = x2 + 1. Encontrar f
(0), f(-2), f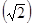 , f(x1
+ Dx). Dx
es una variable que representa un cambio en la variable x.
, f(x1
+ Dx). Dx
es una variable que representa un cambio en la variable x.
Solución
f(x) |
= |
x2 |
+ |
1 |
f(0) |
= |
(0)2 |
+ |
1=1 |
f(-2) |
= |
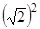
|
+ |
1 = 5 |
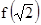
|
= |
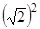
|
+ |
1 = 3 |
f(x1
+ Dx) = (x1
+ Dx)2
1 = 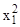 +
Dx + Dx2
+ 1 +
Dx + Dx2
+ 1 |
Las funciones de mayor interés para nosotros son aquéllas cuyo dominio
es un conjunto de números. En este texto, se utilizarán funciones reales
de variable real, es decir el dominio de la función será el conjunto de
los números reales 3
o un subconjunto de él, y el contradominio de f serán 3
o un subconjunto de él.
Si el dominio no se especifica, tomamos como dominio el conjunto más
grande de números reales para el que la función esté definida.
Ejemplo 1.8
Objetivo: mostrar el método para determinar el dominio de una función
cuando x es la variable independiente.
Hallar
el dominio de cada función
Solución.
(A) Como no se puede dividir
por cero, ningún denominador puede igualarse a cero. Por lo tanto, el
dominio de f es el conjunto de todos los números reales excluido el número
2.
Df
= {x| x Î R, x ¹
2} o bien Df = 3
- {2}
(B) El
dominador se factoriza: x2 – x – 6 = (x-3) (x + 2). Este denominador
es cero si x = 3 0 –2; por lo tanto, el dominio es el conjunto de todos
los reales, excluidos el 3 y el –2. Es decir Dg = {x|xÎ 3,
x ¹ -2, 3}
(C) La
raíz cuadrada de un número negativo, no es un número real. Dado que 16
– x es negativo para todo x > 16, el dominio de 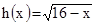 es
x £ 16 o bien (-¥,
16].
es
x £ 16 o bien (-¥,
16].
Definición 1.2
La gráfica de una función f
es el conjunto de todas las parejas (x, f(x)) en un plano coordenado
tales que x es un elemento en el dominio de f.
Las gráficas son muy útiles para describir el comportamiento de f(x)
cuando x varía. También se puede describir la gráfica de f como el conjunto
de puntos P(x, y) tales que y = f(x). Por lo tanto la gráfica de f coincide
con la gráfica de la ecuación y = f(x) y si P(x, y) está sobre la gráfica
de f, entonces la ordenada y es el valor de f en x. Es importante notar
que, como a cada valor de x en el dominio de la función le corresponde
un único valor de y, ninguna recta vertical puede interceptar la gráfica
de la función en más de un punto.
Los
siguientes ejemplos tienen como objetivo el mostrar la gráfica de algunas
funciones elementales.
Ejemplo
1.9. Dibuje la gráfica de f suponiendo que
f(x) = x.
Solución.
En la tabla siguiente aparecen
las coordenadas (x, f(x)) de algunos puntos sobre la gráfica.
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
f(x) |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
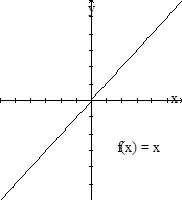
|
Al trazar estos puntos, encontramos que
la gráfica tiene la forma mostrada en la figura.
Ejemplo 1.10
Dada la función f con dominio 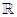 tal que
f(x) = x2 + 1 para toda x en
tal que
f(x) = x2 + 1 para toda x en 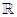 .
Dibuje la gráfica de f.
.
Dibuje la gráfica de f.
Solución.
La gráfica de f consta de todos
los puntos de la forma (x, x2 + 1). En la tabla siguiente
aparecen las coordenadas (x, f(x)) de algunos puntos
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
f(x) |
10 |
5 |
2 |
1 |
2 |
5 |
10 |
Trazando estos puntos llegamos
a la figura mostrada |
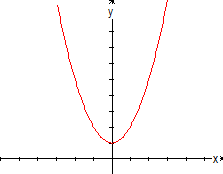 f(x)
= x2 + 1 f(x)
= x2 + 1
|
Ejemplo 1.11
Dibuje la gráfica de f suponiendo que
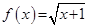
Solución.
Los valores de x tales que x +
1 < 0 no pertenecen al dominio de f ya que en esta caso f(x)
no es un número real. En consecuencia no hay puntos de la forma
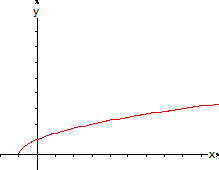
(x, y) con x <-1 en la gráfica de f. En la tabla siguiente
se muestran algunos puntos (x, f(x)) sobre la gráfica:
|
|
Al trazar estos puntos se obtiene la figura
mostrada.
Ejemplo 1.12
Dibuje la gráfica de 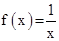
Solución
Como
no se puede dividir por cero, entonces el dominio de f es el conjunto
de todos los números reales diferentes de 0. Si x > 0 entonces
f(x) > 0 por tanto una parte de la gráfica se encuentra en
el primer cuadrante. Si x < 0 entonces f(x) es negativo por
lo tanto otra parte de la gráfica se encuentra en el III cuadrante.
Si x toma valores muy cerca de cero, entonces f(x) = 1/x toma
valores muy grandes en valor absoluto si x toma valores muy grandes
en valor absoluto entonces f(x) = 1/x adquiere valores cercanos
a cero.
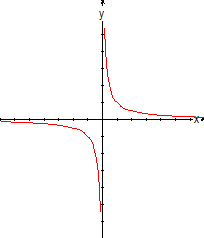
Utilizando las observaciones anteriores y trazando los puntos
(x, f(x)) de la siguiente tabla obtenemos la figura mostrada.
x |
-6 |
-3 |
-1 |
-1/6 |
1 |
3. |
6 |
f(x) |
-.16 |
-.3 |
-1 |
-6 |
1 |
.3 |
.16 |
|
 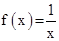
|
Ejemplo 1.1.3
Dibuje la gráfica de f(x) = x3
Solución:
La gráfica de f es el conjunto
de todos los puntos de la forma (x, x3). Trazando los
puntos de la tabla obtenemos la gráfica mostrada
x |
-2 |
-1 |
0 |
1 |
2 |
f(x) |
-8 |
-1 |
0 |
1 |
8 |
|
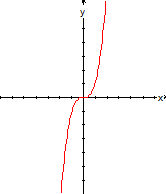
f(x) = x3 |
Ejemplo 1.14
Dibuje la gráfica de f(x) = 3.
Solución.
Si f(x) = 3 entonces la gráfica
de f es el conjunto de parejas (x, 3) y representan una línea
horizontal.
El dominio de f es todo 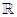 y
el rango {3}. La tabla siguiente muestra algunos puntos sobre
la gráfica de f. y
el rango {3}. La tabla siguiente muestra algunos puntos sobre
la gráfica de f.
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
f(x) |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
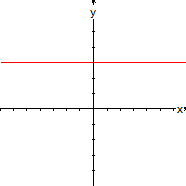
f(x)
= 3 |
|
| |
|
|
|
Ejemplo 1.15
Dibuje
la gráfica de f(x) = |x|.
Solución.
Si x ³
0 entonces f(x) = x por lo tanto la parte de la gráfica a la derecha
del eje coincide con la gráfica de y = x. Si x < 0 entonces
f(x) = -x y por lo tanto la parte de la gráfica a la izquierda
del eje coincide con la gráfica de y = -x. la gráfica es la figura
mostrada. |
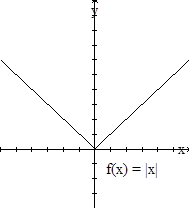
|
Ejemplo 1.16
Dibuje
la gráfica de la función definida de la siguiente manera
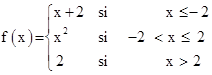
|
Solución.
Si x £
-2 entonces f(x) = x + 2. Esto significa que para x £
-2 la gráfica de f coincide con la gráfica de la recta y = x +
2. Si –2 < x £ 2
entonces f(x) = x2, por tanto esta parte de la gráfica
coincide con la gráfica de la parábola x = y2. Si x
> 2 entonces la gráfica de f es una semirrecta horizontal separada
por una distancia de 2 unidades del eje x. La gráfica es la figura
mostrada. |

|
Se dice que dos funciones f y g de X a
Y son iguales y se escribe f = g, siempre y cuando f(x) = g(x) para toda
x en Y.
Por ejemplo sean:
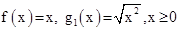
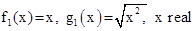
Puesto que 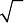 representa
solamente la raíz cuadrada no negativa, entonces f = g pero f1
¹ g1 Haciendo
representa
solamente la raíz cuadrada no negativa, entonces f = g pero f1
¹ g1 Haciendo
f2 (x)
= |x|, x real
se deduce que f2 = g1
En la tabla del ejemplo 1.3 se ve que
la función envía dos elementos distintos del dominio a un mismo elemento
del contradominio, f (-1) = 2, f (1) = 2. Es decir, dos elementos distintos
del dominio tienen la misma imagen. Si las imágenes fueran siempre diferentes,
entonces a la función se le llama uno a uno.
Definición 1.3
Una función de X en Y es
una función uno a uno si siempre que x1
¹ x2 en X
entonces f(x1) ¹
f(x2) en Y.
Si f es uno a uno entonces cada f(x) en
el rango es la imagen de exactamente un x en X. Si todo elemento del contradominio
Y es imagen de algún elemento del dominio X y f es uno, a uno, se dice
que hay una correspondencia uno a uno entre X y Y. Un ejemplo de la correspondencia
uno a uno. Un ejemplo de la correspondencia uno a uno es la asociación
de los números reales con los puntos de una recta coordenada.
Ejemplo 1.17.
Sea
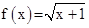 con
x real. Demuestre que f es uno a uno.
con
x real. Demuestre que f es uno a uno.
Solución:
Si x1 ¹
x2 en 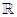 , debemos probar
que f(x1) ¹ f(x2).
Es decir, probar que
, debemos probar
que f(x1) ¹ f(x2).
Es decir, probar que 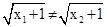 .
Puesto que x1 ¹ x2,
se tiene que x1 + 1 ¹
x2 + 1. De ahí
.
Puesto que x1 ¹ x2,
se tiene que x1 + 1 ¹
x2 + 1. De ahí 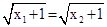 .
Por lo tanto f(x1) ¹
f(x2).
.
Por lo tanto f(x1) ¹
f(x2).
Ejemplo 1.18.
Sea g(x) = x2 + 1, con x real.
Demuestre que g no es uno a uno.
Solución:
La función f no es uno a uno ya que existen
números diferentes en el dominio que tienen la misma imagen. Por ejemplo,
aunque –2 ¹ 2, se tiene que
g (-2) = 5 = g (2).
Si observamos las gráficas de las funciones
de los ejemplos anteriores vemos que en el ejemplo vemos que en el ejemplo
(1.6) donde la función es uno a uno, cualquier recta horizontal corta
a la gráfica de la función en un solo punto. En cambio en la gráfica de
la función g(x) = x2 + 1, cualquier recta horizontal, arriba
del eje de las c, corta a la gráfica en dos puntos.
l
corta en solo un punto
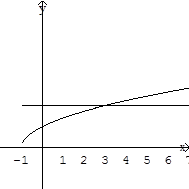
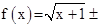
|
l
corta en dos puntos
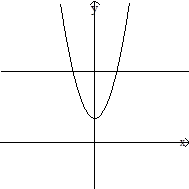
g(x) = x2
+1 |
Definición 1.4
Una función f con dominio
A se llama: I) par, si f (-a) = f(a) para todo número en X,
ii) impar, si f (-a) = -f(a) para toda a en X.
Ejemplo 1.19.
Determine si i)
h(x) = x3, ii)
g(x) = |x| y iii) k(x) = 2x + 1 son funciones pares,
impares o ninguna de las dos.
Solución.
i) Sea
a Î 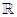 ,
h (-a) = (-a)3 = a3. Puesto que h (-a) = - h(a)
entonces h es impar. Obsérvese que la gráfica de h es simétrica respecto
al origen.
,
h (-a) = (-a)3 = a3. Puesto que h (-a) = - h(a)
entonces h es impar. Obsérvese que la gráfica de h es simétrica respecto
al origen.
ii) Sea
a Î 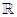 ,
g (-a) = |-a| = g(a). Por lo tanto g es par. Nótese que la gráfica de
g es simétrica con respecto al eje y.
,
g (-a) = |-a| = g(a). Por lo tanto g es par. Nótese que la gráfica de
g es simétrica con respecto al eje y.
iii) Sea
a Î 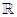 ,
k (-a) + 1 = -2ª + 1. Puesto que k (-a) ¹
k(a) y –k(a), f no es par ni impar. A continuación se muestran las gráficas
de las funciones h, g y k.
,
k (-a) + 1 = -2ª + 1. Puesto que k (-a) ¹
k(a) y –k(a), f no es par ni impar. A continuación se muestran las gráficas
de las funciones h, g y k.
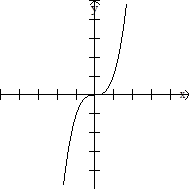
h(x) = x3
Función impar |
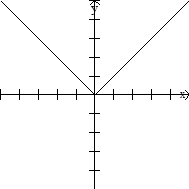
g(x) = |x|
Función par |
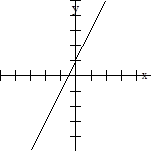
k(x) = 2x +1
No es par ni
impar |

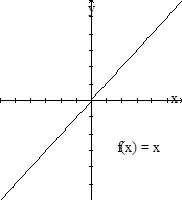
 f(x)
= x2 + 1
f(x)
= x2 + 1