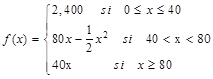Ejemplo 4.5.
Una huerta de manzanos tiene 40 hectáreas por hectárea y el promedio de producción es de 300 manzanas por árbol y por año. Si por cada árbol que se plante por hectárea, además de los 40, la producción promedio disminuye en 5 manzanas, exprésese la producción.
Solución: La producción actual de la huerta puede obtenerse de la siguiente forma: (300)(40) = 12000 manzanas por hectárea y por año, y en general, la producción = (número de árboles por hectárea) (producción promedio anual de un árbol).
Representemos por x el número de árboles plantados, además de los 40. Puesto que la producción promedio por árbol disminuye en 5 manzanas por cada árbol plantado, entonces:
Producción: promedio anual de un árbol = 300 – 5x; y la producción total será:
P = (40 + x)(300-5x)
Obsérvese que 0 £ x £ 60
Ejemplo 4.6.
Se desea construir un recipiente con la forma de un cilindro circular sin tapa con un volumen de 24 p centímetros cúbicos. El precio del material que se usa para el fondo es el triple que el del material que se usa para la parte curva. Exprese el costo del recipiente en función del radio de la base del cilindro.
|
Solución:
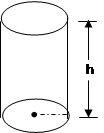
Comenzamos por hacer un dibujo como el mostrado en la figura. Denotamos por r el radio de la base del recipiente y por h la altura (en centímetros). Como el volumen de un cilindro circular es V = py2h y el volumen del recipiente pedido es de 24p cm. cúbicos, entonces tenemos.
|
|
|
pg2 = 24p
Esto nos da la relación
h = 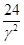
|
El costo total del recipiente es igual al costo de la parte curva más el costo de la base del cilindro.
Si P denota el precio por cm. cuadrado del material que se usa para la parte curva, entonces el precio por cm. cuadrado del material que se usa para el fondo será 3p.
El costo de la parte curva del cilindro es igual al costo del área del rectángulo de base 2pg y altura h, es decir Cc = P(2pg) pero h = 24/g2. Así
|
Cc = P(2pg)(24/g2) = 48pp/g
El costo de la base del cilindro es
Cb = 3p (pg2)
El costo total es
|

|
|
C = Cc + Cb= 48pp /g2 + 3ppg2
C = pp(3g2 + 48 /g) g > 0
|
|
Ejemplo 4.7
Una compañía de autobuses ha adoptado la siguiente política de precios para los grupos que deseen alquilar autobuses. A los grupos que contengan un máximo de 40 personas se les cobrará una suma fija de $2,400.00 (40 veces $60). En grupos que contengan entre 40 y 80 personas, cada una pagará $60.00 menos 50 centavos por cada persona que pase de las 40. La tarifa más baja de la compañía de $40.00 por persona se ofrecerá a grupos que contengan 80 miembros o más. Exprese los ingresos de la compañía de autobuses como una función del tamaño del grupo.
Solución:
Usamos x para denotar el número de personas del grupo y f(x) el ingreso correspondiente. Si 0 £ x £ 40, el ingreso es simplemente f(x) = 2,400. Si x ³ 80, cada persona paga $40.00 y por lo tanto el ingreso correspondiente es f(x) = 40x. La expresión para f(x) cuando 40 < x < 80 es algo más complicada. Comencemos nuestro análisis de esta situación con la relación básica.
Ingresos = (número de personas) (tarifa por persona)
Como x denota el número total de personas del grupo, x – 40 es el número de personas que pasan de 40. La tarifa por persona es la original de $60.00 reducida en ½ peso por cada una de las x – 40 personas extras. Así. Tarifa por persona = 60 – 1/2 (x – 40) = 80 - 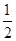 x.
x.
Para obtener el ingreso, simplemente multiplicamos esta expresión por x, el número de personas del grupo. Así para 40 < x 80, f(x) = 80x – 1/2x2.
Podemos resumir todos los tres casos en forma compacta como sigue:
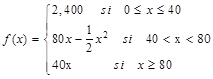
Aunque esta función f(x) está definida para todos los valores no negativos de x, representa el ingreso de la compañía de autobuses solamente cuando x es un entero no negativo.
4.1 Resumen:
La mejor manera de desarrollar una habilidad para tratar con problemas verbales es practicar intensamente. Como los tipos de aplicaciones son muchos y muy variados, es difícil dar reglas específicas para hallar las soluciones. Los siguientes consejos son útiles en muchos casos.
1. Lea el problema cuidadosamente varias veces y fíjese en los datos y en las incógnitas que deben encontrarse.
2. Si es posible, haga un dibujo o un diagrama que incluya los datos pertinentes. Introduzca variables para denotar las incógnitas. Palabras como “que”, “encuentre”, “cuanto”, “donde” y “cuando” deben guiarle para reconocer las incógnitas.
3. Tratar de descomponer el problema en otros más pequeños.
4. Escriba una lista de hechos conocidos y relaciones entre las variables. Una relación entre variables generalmente se escribe como una ecuación.
5. Puede ser útil encontrar el valor de la función para uno o más valores en la variable de manera que pueda generalizarse el procedimiento.
6. Si la elección de variables desemboca en una función indebidamente complicada, considérese otra alternativa.

![]()