1. FUNCIONES Y SUS GRAFICAS.
Una
de las grandes inquietudes de los seres humanos a través de la historia
ha sido la de describir los fenómenos naturales, sus cambios y las relaciones
entre unos y otros. Desde hace tiempo, el hombre ha estudiado ciertos
fenómenos naturales y ha expresado este conocimiento a través de fórmulas
que interrelacionan las magnitudes que caracterizan a dichos fenómenos;
por ejemplo:
Ejemplo 1.1. Para
una cierta dosis de x centímetros cúbicos de una droga la presión sanguínea resultante
P está dada por:
B = 0.5x2
– 0.3x3
Ejemplo 1.2. El
interés sobre una inversión de $4000.00 a razón de 40% anual está dado
por:
I = 0.40 (4000) t
donde t es el número de años.
Ejemplo 1.3. La
ley de Boyle establece que para un gas ideal a temperatura constante,
si el volumen es de v unidades, la presión P es igual a:
P = k/v
siendo k un número fijo.
Ejemplo 1.4. Cuando
se producen x toneladas de una cierta mercadería, el producto recibe un
beneficio de $ B pesos por mes, siendo:
B = 1500 + 15x2
– x3
Este tipo de relaciones motivaron el origen
del concepto de función.
En
cada uno de los ejemplos anteriores se encuentra una variable que depende
de otra; así vemos que:
en el ejemplo 1), la presión sanguínea
P depende de la dosis de x
en el ejemplo 2), el interés depende del
número de años t
en el ejemplo 3), la presión P del gas
depende de las unidades del volumen v
en el ejemplo 4), el beneficio B depende
de las x toneladas producidas.
En otros términos:
La
presión sanguínea P está en función de x
El
interés I está en función de t
La
presión P del gas está en función de v
El
beneficio B está en función de x.
Por esta razón es común llamar a x, t,
v, x variables independientes y a P, I, P, B variables dependientes respectivamente.
Consideremos el ejemplo 1.2.
El interés sobre una inversión de $4000.00
a razón de 40% anual está dado por:
I = 0.40 (4000) t
donde t es el número de años.
Calculemos el interés para distintos valores
de t.
Para |
t=½año |
I=0.40 |
(40000)(1/2) |
=800 |
|
t=
1año |
I
= 0.40 |
(40
000) (1) |
=
1600 |
|
t
= 1.5 año |
I
= 0.40 |
(40
000) (1.5) |
=
2400 |
Siguiendo el procedimiento anterior, obtenemos
la siguiente tabla:
Años
t |
0 |
1/2 |
1 |
1.5 |
2 |
3 |
4 |
Interés1 |
0 |
800 |
1600 |
2400 |
3200 |
4800 |
6400 |
en la cual se observa que a cada valor
de la variable independiente t le corresponde un único valor de la variable
dependiente I. Este tipo de correspondencia es el que caracteriza a una
función. Obsérvese además que tanto la variable independiente t como la
variable dependiente I toma sólo valores mayores que cero, puesto que
en este problema no tiene sentido hablar de tiempos e intereses con valores
negativos.
El
conjunto de valores posibles que puede tomar la variable independiente se
llama dominio de la función y los valores correspondientes de la
variable dependiente forman el conjunto de imágenes de la función
o rango de la función.
Ahora
daremos la definición de función:
Definición 1.1.
Una función
f de un conjunto X a un conjunto Y es una regla de correspondencia que
asocia a cada elemento x de X un único elemento y de Y. El elemento y
se llama la imagen de x bajo
f y se denota por f(x). El conjunto X se llama el dominio de la función
y el conjunto Y contradominio. El rango de la función consta de todas
las imágenes de los elementos de X
Ejemplo 1.5.
Objetivo: Ilustrar el concepto de función.
Ejemplo A. Representemos por y la
distancia en metros que una piedra recorre al caer desde un edificio en
x minutos.
x (tiempo) |
0 |
1 |
2 |
3 |
y
(distancia) |
0 |
2 |
4 |
6 |
Ejemplo B. Sea C = {(1,2), (1,-2),
(3,6)}
Ejemplo C. Sea D = {(1,3), (2,3),
(-1,3), (-2,3)}
Verificar si en cada ejemplo se cumple
la definición de función
Solución:
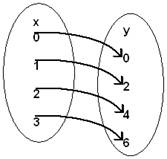
(A) Puesto que a cada x (tiempo) le corresponde un único
valor y (distancia), la correspondencia del ejemplo A es una función.
Esta correspondencia puede expresarse usando parejas ordenas de
la siguiente manera: (0,0), (1,2), (2,4), (3,6) donde cada primer
elemento de la pareja representa el tiempo y cada segundo elemento
una distancia, y puede representarse gráficamente utilizando |
|
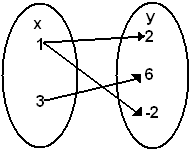
(B)
El conjunto C no representa una función. Nótese que el conjunto
C contiene las parejas ordenadas (1,2) y (1,-2); esto significa
que al número 1 se le asocian dos números distintos 2 y –2. Por
lo cual C no cumple con la definición de función.
La representación gráfica del
conjunto C usando diagramas es la siguiente |
|
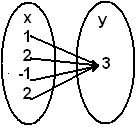
(C) El conjunto D representa una función. La
representación gráfica del conjunto
D = {(1,3), (2,3), (-1,3), (-2,3)} es: |
|


