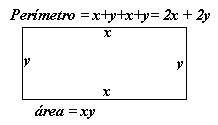B. Información acerca de las cuadráticas
La gráfica de la función cuadrática f(x) = ax2 + bx + c es una parábola que se abre hacia arriba si a > 0, y hacia abajo si a < 0. El vértice de esta parábola tiene la coordenada x dada por x = -b/2a, la coordenada y es f(-b/2a). La intersección de la parábola con el eje x (raíces) se encuentra con la fórmula general ![]() , si ésta tiene intersecciones.
, si ésta tiene intersecciones.
Problema. 30.
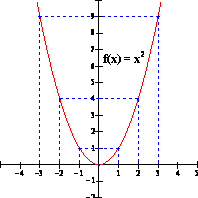
Graficar f(x) = x2.
Para graficar una función no lineal, simplemente escoja algunos valores representativos x del dominio; encuentre f (x) para cada valor, que regularmente se conoce como y en la gráfica; y grafique los pares ordenados resultantes [x, f(x)], y después conecte estos puntos con una línea suave. El procedimiento se ilustra abajo.
|
x |
f(x) = x2 = y |
Puntos |
|
|
-3 -2 -1 0 1 2 3 |
f (-3) = (-3)2 = 9 f (-2) = (-2)2 = 4 f (-1) = (-1)2 =1 f (0) = (0)2 = 0 f (1) = (1)2 =1 f (2) = (2)2 = 4 f (3) = (3)2 =9 |
(-3, 9) (-2, 4) (-1, 1) (0, 0) (1, 1) (2, 4) (3, 9) |
Problema. 31.
|
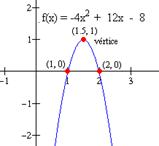
Graficar la función f(x) = -4x2 + 12x -8. En primer lugar, en este caso los valores de los parámetros de la cuadrática son a = -4, b = 12 y c = -8. Ahora, la gráfica es una parábola que se abre hacia abajo puesto que el coeficiente de x2 es negativo. Su vértice tiene coordenada x dada por |
|
|
Las raíces de la parábola se encuentran con la fórmula general
De donde se obtienen los valores de dos raíces de la cuadrática, x = 1 y x = 2. Así, las intersecciones con el eje x, son (1, 0) y (2, 0). |
|
Problema. 32.
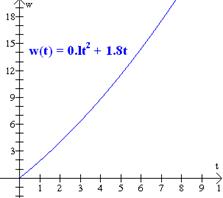
Suponer que se estima que la cantidad de desperdicios echados a un río es una función cuadrática del tiempo. Si se tiraron 11.5 ton en un periodo de 5 días, y 20.8 ton después de 8 días, hallar la cantidad tirada en t días.
La primera oración nos dice que la función de desperdicio es de la forma:
w(t) = at2 + bt + c
Podemos hallar a, b, c para los que son necesarias tres condiciones. Son
tres precisamente las que tenemos:
cuando t = 0, w = 0;
cuando t = 5, w = 11.5
cuando t = 8, w = 20.8
|
Al sustituir estos pares de valores para t y w en la función de desperdicios se tendrá 0=a∙0+b∙0+c, así que c = 0 11.5 = 25a + 5b (2) 20.8 = 64a + 8b (3) Resolviendo simultáneamente el sistema de ecuaciones (2) y (3) encontramos a = 0.1 y b = 1.8 La función buscada es pues, w(t) = 0.lt2 + 1.8t |
|
Problema. 33.
Encontrar el área y las dimensiones del mayor campo rectangular que puede cercar con 300 metros de malla.
|
Solución: Denotemos por x el largo y por y el ancho del campo, como se muestra en la figura. Puesto que el perímetro es el largo de la malla, 2x + 2y = 3000. Por lo tanto 2y = 3000 – 2x y y = 1500 – x. En consecuencia, el área es, A = xy = x(1500 – x) = 1500x – x2 +1500x. |
|
|
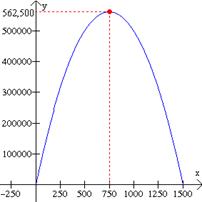
El área mayor posible es el valor máximo valor de la función cuadrática A(x) = -x2 + 1500x. El máximo ocurre en el vértice de la gráfica de A(x). La coordenada del vértice es Por lo tanto la coordenada y del vértice, el máximo valor de A(x) es: A(750) = -7502 + 1500×750 = 562,500 metros cuadrados. El máximo ocurre cuando el largo es x = 750. En este caso el ancho es y = 1500 – x = 1500 – 750 = 750. |
|
Problema. 34.
|
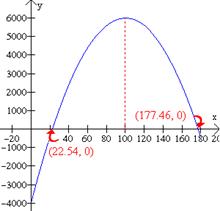
Las ganancias G de una fábrica de reactivos químicos para cada unidad x vendida se ha calculado como G(x) = 200 – x² - 4000 la cual, completando el cuadrado, se puede expresar como G (x) = - (x – 100)² + 6000 La gráfica de G es una parábola que abre hacia abajo, con vértice en (100, 6000), que significa que, cuando se venden 100 unidades, la ganancia se maximiza en $ 6000.
|
|