6. Composición de Funciones.

Problema. 56.              

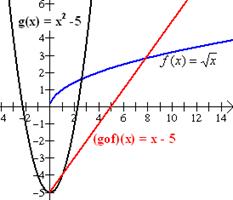
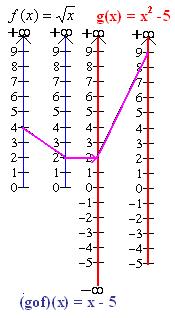
Si  y g(x) = x2 -5, calcular (gof) y su dominio Solución: Tenemos, Aunque x-5 está definida para todos los números reales, el dominio de gof no es el conjunto de los números reales. El dominio de g es el conjunto de todos los números reales y su rango el intervalo [-5, +∞), pero la función  sólo está definida para los números x ≥ 0 y su rango es igual. Así que el dominio de gof es el conjunto de los números reales positivos, es decir, el intervalo (0, +∞). Observa la representación de los dominios de las funciones f, g, y gof de la derecha y la grafica de las tres funciones abajo.

Problema. 57.              

Sean f(x) = x² – 2x, y  g(x) = x  + 3. Encontrar las funciones compuestas (a) (fog)(x), y (b) (gof)(x) y sus dominios.

Solución: Tenemos

(a) (fog)(x) = f(g(x)) = f(x+3) = (x + 3)² – 2(x+3) = x² + 6x + 9 – 2x - 6 = x² + 4x +3.

(b) (gof)(x) = g(f(x)) = g(x² – 2x) = (x² – 2x) + 3 = x² – 2x + 3.

El dominio de f y de g son los reales, y por lo tanto también de (fog) y de (gof). Observa que las funciones gof y fog no son iguales.

Problema. 58.              

En un cierto lago, el pez róbalo se alimenta del pez pequeño gobio, y el gobio se alimenta de plankton. Supongamos que el tamaño de la población del róbalo es una función f(n) del número n de gobios presentes en el lago, y el número de de gobios es una función g(x) de la cantidad x de plankton en el lago. Exprese el tamaño de la población del róbalo como una función de la cantidad de plankton, si  y g(x) = 4x + 3.
 

Solución: Tenemos que n = g(x). Sustituyendo g(x)por n en f(n), encontramos que el tamaño de la población de róbalos está dado por

 

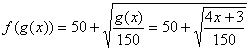
Problema. 59.              

Sea f(x) = 4 y g(x) = -2x² -6x. Calcular: (a) (fog)(x), (b) (gof)(x) y sus dominios.

Solución:

(a) (fog)(x) = f(g(x)) = f(-2x² -6x) = 4.

(b) (gof)(x) = g(f(x)) = g(4) = -2(4)² – 6(4) = -56.

Puesto que el dominio de las funciones f y g son los números reales, el dominio de las funciones fog y gof también son los números reales.

Problema. 60.              

Sean h(x) = -2 y m(x) = 5. Calcular: (a) (hom)(x), y (b) (moh)(x) y sus dominios.

Solución:

(a) (hom)(x) = h(m(x)) = h(5) = -2

(b) (moh)(x) = m(h(x)) = m(2) = 5

Puesto que el dominio de las funciones h y m son los números reales, el dominio de las funciones compuestas hom y moh también son los números reales.

Problema. 61.              

Sean f(x) = x² -1 y g(x) = x + 2. Calcular: (a) (fog)(-2), (b) (fof)(0), (c) (gof)(3), (d) (gog)(-1).

Solución:

(a) (fog)(-2) = f(g(-2))= f(-2 +2) = f(0) = (0)² – 1 = -1

(b) (fof)(0) = f(f(0)) = f( (0)² – 1) = f(-1)= (-1)² – 1 = 1-1 = 0

(c) (gof)(3) = g(f(3)) = g( (3)² -1) = g( 9 – 1) = g(8) = 8 + 2 = 10

(d) (gog)(-1) = g(g(-1)) = g(-1 + 2) = g(1) = 1 + 2 = 3

Problema. 62.              

Si , entonces f puede ser considerada como una función compuesta gof, donde f(x) = 2x² -1 y , así:
 

.

Otra forma de considerar como una función compuesta es considerar las siguientes dos funciones f(x) = 2x² y , de esta manera:
 

.
 

Problema. 63.              

Sea f(x) = (2x + 3)⁵ . Encuentre dos funciones f y g tal que F = fog.

Solución: Esto se puede hacer de más de una forma, pero la forma más natural es la siguiente:

F(x) = 2x + 3    y    g(x) = x⁵

Entonces (gof)(x) = g(f(x)) = (2x + 3)⁵ = F(x)

Problema. 64.              

Un charco circular de agua se está evaporando y disminuye lentamente su tamaño. Después de t minutos, el radio del charco mide  pulgadas; en otras palabras, el radio es una función del tiempo. El área A del charco está dado por A = pr², es decir, el área es una función del radio r. Podemos expresar el área como una función del tiempo sustituyendo en la ecuación del área.

Lo anterior nos permite formar la función compuesta fog, donde f(r) = pr² y g(t) = :

 

Cuando el área se expresa en función del tiempo, es fácil calcular el área del charco en cualquier tiempo. Por ejemplo, después de 10 minutos el área de charco es

 

Problema. 65.              

Los defensores del medio ambiente han estimado que el nivel promedio de monóxido de carbono en el aire es M(m) = (1 + 0.6m) partes por millón cuando el número de personas es m-miles. Si la población en miles en el momento t es P(t) = 400 + 30t + 0.5t², (a) exprese el nivel de monóxido de carbono en el aire como una función del tiempo y (b) calcule el nivel de monóxido de carbono en t = 5.

Solución: (a) Para expresar el monóxido de carbono en función del tiempo se requiere establecer la función compuesta (MoP)(t) = M[P(t)]. Sustituyendo P(t) en M(m), tenemos:

M[P(t)] = M[400 + 30t + 0.5t² ] = 1 + 0.6(400 + 30t + 0.5t²) = 241 + 18t + 0.09t²

(b) Se nos pide evaluar la función compuesta en t = 5.

M[P(5)] = = 241 + 18(5) + 0.09(5)² = 333.25  ppm.

Problema. 66.              

Se conoce que la población de ranas R calculada en miles en una determinada región depende de la población de insectos m en millones. La población de insectos I a su vez varía con la cantidad de lluvia c dada en centímetros. Si la población de ranas es  y la población de insectos es I(c) = 43c + 7.5. (a) Exprese la población de ranas como una función de la

lluvia y (b) estime la población de ranas cuando la lluvia es de 1.5 centímetros.

Solución: (a) Para expresar la población de ranas en función de la lluvia se requiere establecer la siguiente función compuesta (RoI)(c) = R[I(c)]. Sustituyendo I(c) para cada caso de c en R(m), se tiene:

 

(b)
 

Cuando la lluvia es de 1.5 centímetros la población de ranas es aproximadamente de 68000 ranas.