C. Asíntotas verticales y horizontales.

La función tiene una asíntota vertical en todo número que es una raíz del denominador h(x), pero no del denominador g(x).

La función racional cuyo numerador tiene grado n y denominador grado k, tiene:

(a) Una asíntota horizontal en la recta y = a/c, si n = k.

(b) Al eje x como una asíntota horizontal, si n < k, y,

Problema. 42.

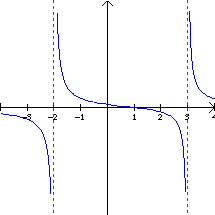
Encuentra las asíntotas verticales y horizontales de la función

Solución: Primero factoricemos el denominador de la función para encontrar las raíces.

La forma factorizada de la función nos permite leer la información necesaria.

Asíntotas verticales: los valores x = -2, y x = 3, son raíces del denominador pero no del numerador, por lo tanto son asíntotas verticales. Asíntotas horizontales: puesto que el denominador tiene un grado mayor que el numerador, el eje x es una asíntota horizontal de la función. Ver grafica de la derecha.

Problema. 43.

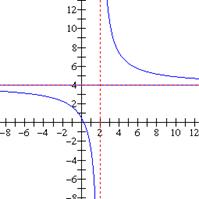
Encontrar las asíntotas de la siguiente función:

Solución: Asíntotas verticales: El valor x = 2, es una raíz del denominador pero no del numerador, por lo tanto es una asíntota vertical.

Asíntotas horizontales: puesto que el denominador tiene el mismo grado que el numerador, la recta y = 4 es una asíntota horizontal. Ver la grafica de la derecha.

Problema. 44.

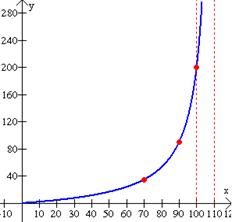
Suponga que el costo C en miles de dólares de la expulsión de x por ciento de dióxido de azufre del escape de una planta de fundición de cobre se expresa con la función racional

Hallando la asíntota vertical, aunque sea por fuera del dominio limitado, y graficando se pueden observar los costos elevados de la limpieza de la parte final del agente contaminante.