|
O sea, el valor del límite de una función en un punto es
único.
En los apartados anteriores hemos determinado el límite de una función en un punto, utilizando para ello la representación gráfica de la función. Sin embargo, se hace necesario poseer otros criterios que permitan agilizar el proceso. Con este fin es que estudiaremos algunos teoremas básicos para determinar el límite de una función en un punto.
|
O sea, el valor del límite de una función en un punto es
único.
|
Ejemplos:
Ejercicio:
Determine cada uno de los siguientes límites:
Como consecuencia del teorema anterior se tiene que:
| a. |
|
| b. |
|
Ejemplos:
|
Ejemplos:
Ejercicio:
Determine cada uno de los límites siguientes:
| Teorema 4 | |
| Si
|
Ejemplos:
Ejercicio:
Determine los límites indicados.
| Teorema 5 | |
Si |
Este teorema lo que nos dice es que el límite de la suma de dos funciones,
es igual a la suma de los límites de cada una de las funciones.
Ejemplos:
Ejercicio:
Determine los límites siguientes:
El teorema anterior puede extenderse a un número cualquiera finito de funciones.
| Teorema 6 | |
Si |
Es decir, el límite del producto de dos funciones es igual al producto de los límites de cada una da las funciones. Ejemplos:
Ejercicio:
Determine el valor de cada uno de los límites siguientes:
El teorema anterior puede extenderse a un número cualquiera finito de funciones
| Corolario | |
Si |
Observe que
![]() (n factores) por lo que aplicando el teorema anterior se tiene que:
(n factores) por lo que aplicando el teorema anterior se tiene que:
![]()
![]()
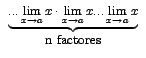
![]() (n factores)
(n factores)
![]()
Ejemplos:
En particular, el límite de la enésima potencia de
![]() es igual a la
enésima potencia del límite de
es igual a la
enésima potencia del límite de
![]() . Es decir
. Es decir
![]()
Ejemplos:
| Teorema 7 | |
Si |
| Teorema 8 | |
Ejemplos de los teoremas 7 y 8
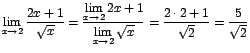 (se aplicaron los teoremas 2 y 4)
(se aplicaron los teoremas 2 y 4) 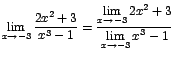 (por teorema 7)
(por teorema 7) 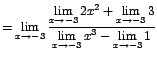 (por teorema 5)
(por teorema 5) Observe que en este ejemplo se han aplicado directamente los teoremas estudiados, sin hacer el desglose paso por paso como en el ejemplo anterior.
Ejercicio:
Determine el valor de cada uno de los siguientes límites:
| Teorema 9 | |
Si (1) (2) |
Ejemplos:
| Teorema 10 |
| Si
|
| (1)
|
| (2)
|
Ejemplos:
Ejercicio:
Determine el valor de cada uno de los siguientes límites:
![$\displaystyle {\lim_{x \rightarrow{4}}{\sqrt[4]{\frac{x^{2}+1}{2}}}}$](images/img269.gif)