Definición: El valor absoluto de un número real x lo denotamos por |x| y lo definiremos como sigue:
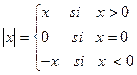
Introducción al Cálculo Diferencial e Integral
Números Reales
Definición: El valor absoluto de un número real x lo denotamos por |x| y lo definiremos como sigue: |
|
Observa que |x| siempre es un número real positivo o cero. Además -|x|< x < |x|.
1. Ejemplo: (a) |-5| = - (-5) = 5. (b) |3| = 3 (c) |-3| = -(-3) = 3 (d) |0| = 0 (e) | (f) Exprese
|4x – 2| sin emplear el símbolo de valor absoluto. Esto
es,
(g) Para encontrar |p - 6|, observa que p » 3.14 así que p - 6 < 0. Por lo tanto, |p - 6| se define como la parte negativa de p - 6, esto es |p - 6| = -(p - 6) = -p + 6 (h) (i) |
Sean a y b dos números reales, entonces,
|
1.
|
3.
|
|
|
2.
|
4.
|
|
2. Ejemplo: (a) |(-7)∙3| = |-7|∙|3| = 21 (b) |4-2| = |2-4| = 2 (c) |(-6)(-3)| = |-7| ∙ |-3 | = 7∙3 = 21 (d) |8 - x | = |x - 8 | (e) (f) (g) |5(2 - 4) + 7| = |5(-2) + 7 | = | -10 + 7| = | -3 | = 3 (h) 4 - | 3 - 9| = 4 - | -6 | = 4 – 6 = -2 (i) | (-6)2 | = | 36 | = 36 (j) | -6 |2 = (6)2 = 36 (k) | (-6)2 | = | -6 |2 . Por los ejemplos i y j. (l) |3 -p| = |-1(-3 + p)| = |-1(p - 3)| = |-1| |p - 3| = 1|p - 3| = p - 3. Puesto que p - 3 > 0 |
|||
Cuando los números reales son representados geométricamente sobre un eje real, el número |x| se llama la distancia de x a 0. Es decir, el valor absoluto nos sirve para medir la distancia de un número al cero. | a | es la distancia entre a y 0. Así, | 6 | representa la distancia que hay entre el 0 y el número 6.
![]()
Definición: La distancia entre dos puntos de la recta a y b se define como |a – b|.
Nota: Observa que |a – b| = |b – a|, es decir, que la distancia de a a b es la misma distancia de b a a.
3. Ejemplo: (a) La distancia entre – 6 y 8 es la misma que entre 8 y – 6: |8 – (-6)| = |14| = 14 unidades, |(- 6) – 8| = |-14| = 14 unidades. (b) La
distancia entre 4.2 y 9 es |4.2 - 9 | = |-4.8| = 4.8 (c) La distancia entre x y 5 es igual a tres: | x - 5| = 3 (d) La distancia entre x y 6 es menor que 4: | x - 6| < 4 (e) La distancia entre x y -5 es menor que 6: |x – (-5)| = | x + 5|< 6 (f) La distancia entre x y 7 es mayor que 12: |x - 7| > 12 (g) La distancia entre x y -3 es mayor o igual que 3: |x – (-3)| = |x + 3| ≥ 3 |
|
4. Resolver la ecuación | x - 5 | = 3. |
|
Solución: Esta expresión es equivalente a “la distancia entre x y 5 es igual a 3”. Puesto que x es un número real, entonces x puede estar a la izquierda o la derecha de 5. Observa la figura. ←→
La figura nos muestra que sólo hay dos números cuya distancia a 5 es de 3 unidades, y estos son x = 2 y x = 8. De esta manera la solución a la ecuación son estos dos números. |
|
5. Resolver la ecuación | x - 5 | ≤ 7. |
Solución: Esta expresión es equivalente a “la distancia entre x y 5 es menor o igual a 7”. Puesto que x es cualesquier número real, entonces x puede estar a la izquierda o la derecha de 5. Observa la figura.
La figura nos muestra que los números cuya distancia a 5 es menor o igual a 7 unidades están en el intervalo -2≤ x ≤ 12. Así que la solución a la desigualdad está dada por este intervalo. Por ejemplo x = -1 es solución, puesto que | -1- 5 | = | -6 | = 6 ≤ 7. |
6. Resolver la ecuación | x - 5 | ≥ 7. |
Solución: Esta expresión es equivalente a “la distancia entre x y 5 es mayor o igual a 7”. Puesto que x es cualquier número real, entonces x puede estar a la izquierda o la derecha de 5. Observa la figura.
La figura nos muestra que los números x cuya distancia a 5 es mayor o igual a 7 unidades están en el intervalos x ≤ -2 y x ≥ 12. Así que la solución a la desigualdad está dada por los intervalos (-∞, -2] y [12, +∞). Por ejemplo x = 15 es solución, puesto que | 15- 5 | = | 10 | = 10 ≥ 7. |