Un estudiante
debe mantener un promedio numérico final en cinco exámenes de
80% a 89%, para obtener una nota final de B en el curso de cálculo.
Si en los primeros cuatro exámenes obtuvo calificaciones de 96%,
70%, 81% y 95%, ¿qué calificación deberá obtener en el examen
final para obtener una nota de B?
Dejemos que x(0 ≤ x ≤ 100)
sea la calificación que debe obtener el estudiante en el examen
final. Un promedio se busca sumando las notas y dividiendo entre
el número de notas. Así, el promedio del estudiante se calculará
de la siguiente manera:
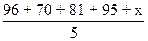
Queremos que el promedio final quede entre 80% y 90%, inclusive
el 80. Luego, al simplificar la expresión anterior, tenemos:
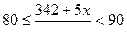
Si resolvemos la desigualdad anterior:
400
≤ 342 + x < 450
58 ≤ x < 108
El resultado anterior significa
que, el estudiante no puede sacar menos de 58% en el examen
final si desea una calificación de B en dicho curso. Otras consecuencias
del resultado anterior son
que si obtiene una calificación menor de 58% en dicho examen final,
su nota final será menos de B y que no hay modo de que el estudiante
obtenga una nota final de A, pues 0 ≤ x ≤ 100
y el resultado obtenido implica que tendría
que obtener una calificación mayor o igual a 108 para obtenerla. |
![]()