8. Desigualdades lineales simultáneas
Al
resolver desigualdades lineales simultáneas, debemos tener presente
que lo que estamos buscando es la
intersección de los conjuntos solución de
un sistema de dos o más desigualdades. Esto puede lograrse con la
máxima facilidad graficando las desigualdades
y observando la intersección
de sus gráficas. Si la intersección
es vacía no hay soluciones simultáneas.
Ejemplo
7. Resuélvase, graficando,
el sistema de desigualdades lineales
2x
- y + 4 < 0
x
+ y + 1 ≥ 0
Solución.
Primero despejamos y en cada una de las desigualdades para obtener
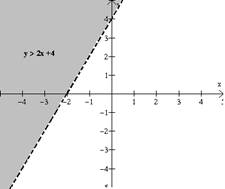
y
> 2x +4
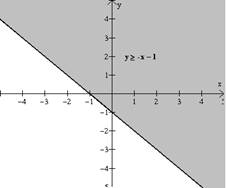
y
≥ -x – 1
Luego graficamos la recta y = 2x +4 para obtener
el conjunto solución de la desigualdad 2x - y + 4 < 0 figura 7.1
Figura
7.1 |
Figura
7.2 |
|
Después graficamos
la recta y = -x -1 para obtener la solución grafica de la desigualdad
y ≥ -x – 1, ver figura 7.2.
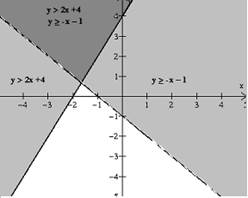
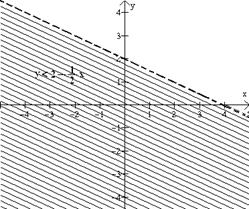
Para encontrar la solución del sistema
unimos las dos graficas en un mismo sistema de coordenadas. La
solución se encuentra en la intersección de los dos conjuntos
solución como se muestra en la figura 7.3.
|
|
Ejemplo 8. Resuélvase,
graficando, el sistema de desigualdades lineales
2x
+ 2y < 4 (8)
x- y < 0 .
Solución.
Primero despejamos y
en las desigualdades, para obtener:
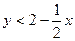 y
y
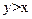
Después graficamos la recta y
= 2 –(1/2)x y debajo de esta recta dibujamos la solución de la desigualdad
y < 2
– (1/2)x, que se muestra en la figura 8.1. Después graficamos en el mismo
eje de coordenadas la recta y = x y sobre esta recta dibujamos
la solución de la desigualdad y >
x. La intersección de las dos soluciones
representa la solución del sistema de desigualdades, figura 8.2
Figura
8.1 |
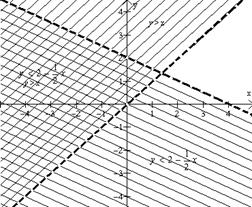
Figura
8.2 |
Ejemplo 9. Una
firma está planeando la producción para la semana
siguiente. Está haciendo dos, productos, X y Y, cada uno de los
cuales requiere cierto número de horas
en fundición, maquinación y acabado de acuerdo a lo que se muestra
en el cuadro 9.1. Durante la semana
que se está planeando, el número de horas de que se va a disponer en cada una de las áreas en cuestión
es el siguiente
Fundición, 110
Maquinación, 150
Acabado, 60
Producto |
Horas
por unidad |
Fundición |
Maquinación |
Acabado |
X |
6 |
3 |
4 |
Y |
6 |
6 |
2 |
Tabla
9.1 |
Grafíquese el sistema de desigualdades lineales que muestra las cantidades de X y Y que pueden ser producidas.
Solución. Como los
productos X y Y requieren,
cada uno, seis horas de trabajo
de fundición por cada unidad producida, y como hay 110 horas disponibles
para tal trabajo, la cantidad total del tiempo de trabajo de fundición
que se utiliza debe satisfacer la relación
6x +6y ≤ 110
dónde x representa el número de unidades del producto X
procesadas y y
el número de unidades del producto Y. Análogamente, las relaciones
pertenecientes a la capacidad de maquinación
y acabado son, respectivamente,
3x
+ 6y ≤ 150
4x + 2y ≤ 60
Aparte de las tres limitaciones a la producción arriba indicadas, hay
dos condiciones adiciónales que cualquier
combinación de producciones debe
satisfacer.
x≥0 y≥0.
Esto
es, la producción no puede ser negativa. La
parte sombreada de la figura 9.1 muestra todas las combinaciones
de producción que satisfacen
todas las restricciones. Obsérvese
que en este problema la capacidad de maquinación no es,
en realidad, ningún tipo de
restricción; es decir, cualquier combinación de producción que
satisface las otras dos limitaciones satisfará también la
capacidad de maquinación. |
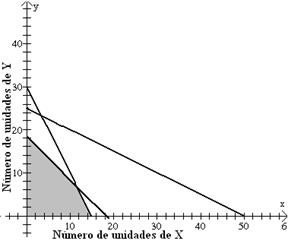
Figura
9.1 |





