Si k es número positivo (k>0) y a, b, y x son números reales entonces:
1.
![]()
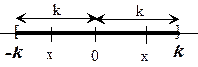
2.
![]()
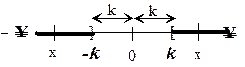
Las propiedades 1 y 2 también son validas si £ se remplaza por <.
3.
Si ![]() , entonces x
= k, o, x = -k.
, entonces x
= k, o, x = -k.

4. ![]() .
.
Introducción al Cálculo Diferencial e Integral
Números Reales
La relación entre el valor absoluto y la distancia nos permite utilizar los valores absolutos para describir desigualdades, y esto nos conduce a las siguientes propiedades:
Si k es número positivo (k>0) y a, b, y x son números reales entonces: |
|
1.
|
2.
|
Las propiedades 1 y 2 también son validas si £ se remplaza por <. |
|
3.
Si
|
4.
|
7. Resolver |2x – 5| = 3. |
|
Solución: Por la propiedad 3de (4), |2x – 5| = 3 es equivalente a las siguientes ecuaciones: 2x – 5 = 3 o 2x – 5 = - 3 |
|
Resolviendo 2x – 5 = 3. Tenemos: 2x = 3 +5 2x = 8 x = 8/2 = 4 |
Resolviendo 2x – 5 = - 3. Obtenemos: 2x = -3 + 5 2x = 2 x = 2/2 = 1 |
De aquí tenemos que la igualdad |2x – 5| = 3 tiene como solución los valores de x = 4 y x= 1.
|
|
8. Resolver |3x + 3| = 15. |
Solución: Por la propiedad 3de (4), |3x + 3| = 15 esta ecuación se cumplirá si 3x + 3 = 15 o bien , -(3x + 3) = 15 |
Resolviendo estas ecuaciones se tiene: 3x =15 - 3 o -3x = 15 + 3. De ahí que x = 4 o x = -6. |
9. Determinar el conjunto de soluciones que satisfaga la desigualdad |x - 5 |< 4. |
Solución: De acuerdo con la propiedad 1 del párrafo 4, la desigualdad en valor absoluto es equivalente a la siguiente desigualdad: -4 < x – 5 < 4 |
Sumando 5 a ambos lados de la desigualdad para despejar x tenemos: -4 + 5 < x – 5 + 5 < 4 + 5 1 < x < 9 |
Por lo tanto la solución es el intervalo abierto (1, 9).
|
10. Determinar el conjunto de soluciones que satisfaga la desigualdad |3x + 2 | ³ 4. |
|
Solución: De acuerdo con la propiedad 2 del párrafo 4, la desigualdad en valor absoluto es equivalente a las siguientes desigualdades sin valor absoluto: (a) 3x + 2 ³ 4 o (b) 3x + 2 £ - 4 |
|
Solución de (a). 3x + 2 ³ 4 3x ³ 4 – 2 x ³ 2/3 o bien [2/3, +∞) |
Solución de (b) 3x + 2 £ - 4 3x £ - 4 – 2 x £ - 6/3 o bien (-¥, -2] |
Por lo tanto la solución es la unión de las dos soluciones: (-¥, -2]È [2/3, +∞).
|
|
11. Evaluar la desigualdad 0 < | x +3| £ 8. |
|
Solución: La desigualdad significa que 0 <|x + 3| y | x + 3| £ 8 |
|
En el primer caso, 0 <|x + 3| es verdadero para todo número real excepto x = -3. Así la solución son todos los números reales menos el -3. Es decir (-∞, -3)È(-3, +¥). |
En el segundo caso se tiene por la propiedad 1 del párrafo 4 que: -8 £ x + 3 £ 8 -8 - 3 £ x £ 8 - 3 -11 £ x £ 5 o bien [-11, 5]. |
Por lo tanto el conjunto de números reales x que satisface ambas desigualdades es la intersección de los dos conjuntos y consta de todos los números en [-11, 5] excepto -3. La solución expresada como unión de intervalos [-11, -3) È (-3, 5].
|
|
12. Encontrar la solución de la desigualdad |x - 5 | ≤ 2x + 2. |
|
Solución: De acuerdo con la propiedad 1 del párrafo 4, la desigualdad en valor absoluto es equivalente a la siguiente desigualdad: -(2x + 2) ≤ x – 5 ≤ 2x + 2 para resolverla la trataremos como dos casos separados. |
|
Caso 1: -(2x + 2) < x – 5. Despejando x tenemos. -2x – 2 ≤ x – 5 -2x -x ≤ – 5 + 2 -3x ≤ – 3 x ≥ –3/-3 o bien, x ≥ 1 Así, la solución es el intervalo [1, +∞). |
Caso 2: x – 5 < 2x + 2. Despejamos x. x – 5 ≤ 2x + 2 x -2x ≤ 2 +5 -x ≤ 7 x ≥ -7 La solución es el intervalo [-7, +∞) |
Ahora, la solución de la desigualdad |x - 5 | ≤ 2x + 2, es la intersección de las soluciones de los dos casos. La intersección de x ≥ 1 y x ≥ -7 es el intervalo, [1, +∞).
|
|