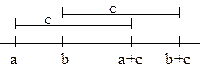I. Desigualdades.

0. Introducción.

Resolver ecuaciones, por ejemplo, ─6x + 17 = 8 o x² - 2x - 5 = 0─ es una de las tareas tradicionales de las matemáticas. Pero es casi de la misma importancia en cálculo saber resolver una desigualdad por ejemplo ─2x + 6 <7 o x² -2x+4 ≥ 0─ Resolver una desigualdad es encontrar el conjunto de todos los números reales que la hacen verdadera. En contraste con una ecuación, cuyo conjunto solución, en general, consta de un número o quizá un conjunto finito de números, el conjunto solución de una desigualdad por lo común consta de un intervalo completo de números o, en algunos casos, la unión de tales intervalos.

1. Propiedades de las desigualdades.

Dados dos números reales, siempre podemos compararlos y decidir si son iguales o cuál es más grande.
Escribimos a < b para decir que a es menor que b y a £ b para decir que a es menor o igual que b.
En la recta, a < b significa que el punto correspondiente a a está a la izquierda del que corresponde a b.

El orden en los números reales tiene las siguientes propiedades:

1. Si a y b son números reales, sucede una y sólo una de las siguientes relaciones (propiedad de tricotomía):

i) a = b; ii) a > b; iii) a < b

2. Si a < b y b < c, entonces a < c (propiedad transitiva).
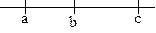
3. Si a < b y c 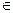IR, entonces a + c < b + c.
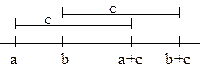
4. Si a < b, y c > 0 entonces ac < bc
5. Si a < b, y c < 0 entonces ac > bc. Podemos tener los tres casos siguientes.
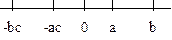
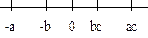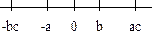
-bc < -ac	bc < ac	-bc < ac

2. Intervalos.

Definición: Dados dos números a, b en IR, con a menor que b, el intervalo definido por a y b es el conjunto de números x en IR que están entre a y b.

Los puntos a y b pueden o no pertenecer al intervalo, entonces podemos tener los siguientes casos:

1. Si a y b pertenecen al intervalo, éste se llama intervalo cerrado y escribimos: [a, b] = {x Î IR ÷ a £ x £ b}.

2. Si a y b no pertenecen al intervalo, éste se llama intervalo abierto y escribimos: (a, b) = {x Î IR ÷ a < x < b}

3. Si alguno de los extremos, pero no ambos, pertenece al intervalo tenemos estos dos casos (intervalos semiabiertos o semicerrados):

La noción de intervalo se puede extender, para denotar al conjunto de las x Î IR que son más grandes o más chicas que un número dado.

Por ejemplo, para denotar al conjunto { x Î IR ÷ x > a} escribimos (a, + ¥ ).

Los siguientes conjuntos son intervalos:

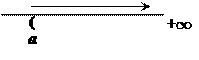
(a, + ¥) = { x Î IR ÷ x > a}
[a, + ¥) = { x Î IR ÷ x ³ a}
( - ¥, b) = {x Î IR ÷ x < b }
( - ¥, b] = {x Î IR ÷ x £ b }
( - ¥, +¥) = IR