.Introducción al Cálculo Diferencial e Integral
Números Reales
Al conjunto formado por los números racionales e irracionales se le
denomina conjunto de los números reales y se designa por .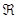
Podemos pues recordar en un diagrama, la relación entre los distintos tipos de números que hemos estudiado a lo largo del documento:
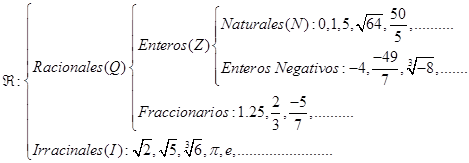
Sabemos que los números racionales se sitúan en la recta de tal manera que en cada tramo de la misma, por pequeño que éste sea, hay infinitos.
Ahora bien, aunque parezca extraño, una vez colocado los racionales en la recta quedan infinitos “huecos” que son ocupados por los irracionales.
Entre todos ellos llenamos la recta, es decir, cada punto de la recta se corresponde con un número real; de ahí el nombre de Recta Real.
Para colocar los números reales sobre la recta se procede así:
Se coloca el cero en un punto cualquiera de la recta.
Se coloca el uno, en un punto arbitrario, a la derecha del cero.
Ahora se coloca cualquier número natural de uno en uno, ordenados de menor a mayor, a la misma distancia que entre cero y uno.
Los enteros negativos se colocan a la izquierda del cero, empezando por -1 y de uno en uno, a la misma distancia que entre cero y uno.
Los infinitos huecos que quedan entre los enteros, serán ocupados por los racionales e irracionales, que se podrán colocar de modo exacto (usando métodos geométricos) o, aprovechando la expresión decimal de los mismos, de modo aproximado (que es el más habitual
La siguiente tabla resume las propiedades de los números reales:
Propiedad |
Operación |
Definición |
Significado |
Cerradura |
Suma
Multiplicación |
|
El resultado de sumar o multiplicar dos números reales, también es número real. |
Conmutativa |
Suma
Multiplicación |
|
El orden al sumar o multiplicar los números reales, no afecta el resultado. |
Asociativa |
Suma
Multiplicación |
|
No importa el orden al asociar la suma o multiplicación de tres o más número reales, el resultado siempre será el mismo. |
Neutro |
Suma
Multiplicación |
|
Si a un número real se le suma el cero (neutro aditivo), se queda igual. Sin un número real se multiplica por 1 (neutro multiplicativo), se queda igual. |
Inverso |
Suma
Multiplicación |
|
Si a un número se le suma su inverso, se obtiene como resultado el 0 (neutro aditivo). Si un número se multiplica por su inverso multiplicativo, se obtiene como resultado 1 (neutro multiplicativo). |
Distributiva |
Suma respecto a la multiplicación |
|
El factor se distribuye a cada sumando. |
Ejemplos
a)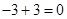 
Elemento
Inverso para la Suma
b)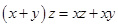 
Propiedad
distributiva
c)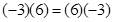 
Propiedad
conmutativa para el producto
