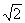; la longitud de la circunferencia, tomando como unidad
su diámetro es el número irracional p
(pi). Introducción al Cálculo Diferencial e Integral
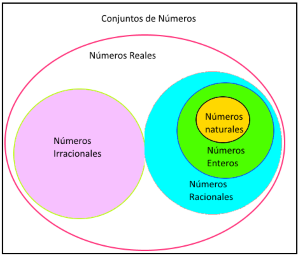
Números Reales
El concepto de números irracionales proviene de la Escuela Pitagórica, que descubrió la existencia de números irracionales, es decir que no eran enteros ni racionales como fracciones. Esta escuela, los llamó en primer lugar números inconmensurables.
La necesidad de los números irracionales surge de
medir longitudes sobre algunas figuras geométricas: la longitud de la
diagonal de un cuadrado tomando como unidad el lado del mismo es 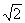; la longitud de la circunferencia, tomando como unidad
su diámetro es el número irracional p
(pi).
La expresión decimal de cualquier número irracional consta de infinitas cifras no periódicas. Existen infinitos números irracionales. Todos ellos, junto con los racionales, forman el conjunto de los números reales.
El filósofo griego Pitágoras de Samos (540 a.C.) descubrió estos números al establecer la relación entre el lado de un cuadrado y la diagonal del mismo.
Por el teorema de Pitágoras, sí l=1, entonces:
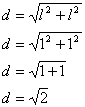Donde
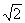es un número irracional.
Así, por ejemplo,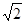 
no se puede escribir como cociente
de dos enteros:
Demostración (reducción al absurdo)
Supongamos que sí se puede y llegaremos a una contradicción.
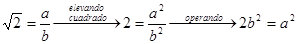
Como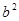 
es
un cuadrado perfecto, contiene el factor (2) un número par de veces. Por
tanto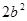 
contendrá
el factor (2) un número impar de veces, lo cual es imposible pues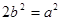 
y
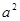es
un cuadrado perfecto.
Los números no racionales se les llaman Irracionales.
Acabamos de ver que 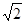es irracional y
en general:
|
Hasta el siglo XVI fue cuando consideraron llamar número irracional a los números con desarrollo decimal infinito no periódico. Algunos de ellos se pueden encontrar al resolver un problema. Como por ejemplo:
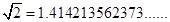
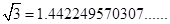
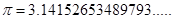
Como se observa en los ejemplos, el desarrollo decimal que presentan estos números es infinito no periódico y con base a la definición planteada en los números racionales, no podríamos expresarlos como un cociente de dos números enteros.
Un número irracional importante es el llamado número (e), en honor al insigne matemático (L. Euler).
Es quizá el número más importante en matemáticas superiores, aparece en numerosos procesos de crecimiento (bacteriano, de una masa forestal,…), aparece también en los procesos físicos de la desintegración radiactiva, en la descripción de la curva catenaria (curva que describe una cadena), y en otras muchas curvas como la que describe la distribución del carácter “talla” de una población estadística (llamada distribución Normal).
En el tema de límites veremos que el número (e) se obtiene como el límite
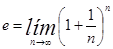
El valor decimal aproximado de este número es: |
Analizando todos los conjuntos que se mencionaron anteriormente, se observa que los Naturales están incluidos en los números Enteros, y éstos a su vez están incluidos en los Racionales. Pero ellos no tienen ninguna relación con los Irracionales, pues bien, todo ellos forman parte de los números Reales, como se muestra en el siguiente diagrama.
