Introducción
El propósito de este material es poner a disposición de los
profesores del nivel medio superior una breve exposición del
tema de CONGRUENCIAS y una selección de problemas de concurso a
todos los niveles: Estatal, nacional (diversos países) y de
Olimpiadas Internacionales.
Este tema de la teoría de los números no es parte de la
currícula de Bachillerato en nuestro estado, sin embargo es tema
de exámenes en concursos nacionales e internacionales, razón
por la cual tenemos que incluirlo en los materiales para preparar
a nuestros estudiantes para las Olimpiadas Estatales y
Nacionales.
Ha sido una tradición proporcionar a los estudiantes que
participan en nuestro estado en la Olimpiada de Matemáticas, una
exposición de esta temática en los talleres de entrenamiento.
Creemos que este tipo de materiales, en manos de profesores
entusiastas, contribuirá a una mejor preparación de nuestros
representantes en las olimpiadas nacionales.
Eduardo Tellechea Armenta
Profesor del Departamento de Matemáticas
Universidad de Sonora.
Octubre de 1998.
C O N G R U E
N C I A S
Con el fin de motivar el concepto de CONGRUENCIA,
analizaremos los siguientes dos problemas.
Problema 1. Se tiene un
edificio de dos pisos con los cuartos numerados como en la figura
1
|
3
|
5
|
7
|
9
|
…
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
Ad.
|
2
|
4
|
6
|
8
|
…
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
¿En que piso localizamos el cuarto No. 98 ?
Solución: En la planta baja (Ad.), pues claramente
observamos que en el primer piso están los cuartos con números
impares y en la planta baja, los de números pares.
Problema 2. Se tiene un
edificio de cinco pisos con los cuartos numerados como en la
figura.
4
|
9
|
14
|
19
|
24
|
…
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
3
|
8
|
13
|
18
|
23
|
…
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
2
|
7
|
12
|
17
|
22
|
…
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
1
|
6
|
11
|
16
|
21
|
…
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
Ad.
|
5
|
10
|
15
|
20
|
…
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
.
|
¿En que piso localizamos el cuarto No. 98?
Solución: En el problema anterior, por su sencillez,
pudimos mentalmente dividir al conjunto de los enteros
(positivos) en dos clases ajenas: pares e impares. En este
segundo problema tenemos que dividirlos en 5 clases ajenas y ser
capaces de ubicar a cualquier entero en alguna de ellas.
Si observamos detenidamente la figura, podemos ubicar a los
cuartos de la siguiente manera:
No. de Piso
Característica
Forma
Primer piso:
Múltiplos
de 5
5k
Segundo piso:
Los que
exceden en una unidad a un múltiplo de 5
5k+1
Tercer piso:
Los
que exceden en dos unidades a un múltiplo de 5
5k+2
Cuarto piso:
Los
que exceden en tres unidades a un múltiplo de 5
5k+3
Quinto piso: Los que exceden en cuatro unidades a un múltiplo
de 5
5k+4.
Después de este pequeño análisis, podemos decir que el
cuarto No. 98 se encuentra en el cuarto piso,
puesto que 98 = 5(19) + 3.
Obsérvese que los del primer piso son aquellos que al
dividirse entre 5 dejan residuo cero, los del segundo piso son
aquellos que al dividirse entre 5 dejan residuo 1 y así
sucesivamente.
Si consideramos el conjunto de los enteros, con este criterio
podemos dividirlos en 5 clases:
C0 = {…, -15, -10, -5, 0, 5, 10, 15,
…}
C1 = {…, -14, -9, -4, 1, 6, 11, 16,
…}
C2 = {…, -13, -8, -3, 2, 7, 12, 17,
…}
C3 = {…, -12, -7, -2, 3, 8, 13, 18,
…}
C4= {…, -11, -6, -1, 4, 9, 14, 119,
…}.
La característica de la clase Cr es que al
dividirse cualquiera de sus elementos entre cinco, deja residuo
r.
Si dos enteros pertenecen a la misma clase, diremos que ellos
son congruentes módulo 4.
En general tenemos la siguiente definición:
DEFINICIÓN.- Decimos que los enteros a
y b son CONGRUENTES MÓDULO m
, m>0 si al dividirse entre m dejan el mismo residuo, y lo
denotaremos como:
a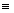 b (mod m)
b (mod m)
Ejemplos. -13 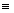 17
(mod 5) pues ambos pertenecen a C2.
17
(mod 5) pues ambos pertenecen a C2.
5 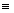 15 (mod 5)
pues ambos pertenecen a C0
15 (mod 5)
pues ambos pertenecen a C0
8 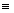 17 (mod 3)
pues al dividirse entre 3, dejan residuo 2.
17 (mod 3)
pues al dividirse entre 3, dejan residuo 2.
PROPOSICIÓN.- a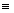 b (mod m) Û m | (b-a).
b (mod m) Û m | (b-a).
Demostración:
a) (Þ)
Si a = mq1 + r y b = mq2 +
r con 0 £ r < m Þ b-a = m(q2 - q1)
Þ m | (b-a).
b) (Ü)
m | (b-a) Þ b-a = mk para
algún entero k
Por el algoritmo de la división a = mq1 + r1
y b = mq2 + r2 con 0 £ r1 < m , 0 £ r1 < m
restando estas igualdades obtenemos:
b-a = m(q2 - q1) + (r2
- r1). Pero como b-a = mk , tenemos que r2
- r1 = 0 y por lo tanto r2 = r..
por lo que a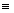 b
(mod m)
b
(mod m)
Teorema: La relación congruencia módulo m tiene
las siguientes propiedades:
a) a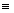 a
(mod m)
a
(mod m)
b) Si a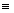 b
(mod m) entonces b
b
(mod m) entonces b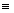 a (mod m)
a (mod m)
c) Si a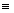 b
(mod m) y b
b
(mod m) y b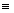 c (mod m) entonces a
c (mod m) entonces a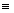 c (mod m)
c (mod m)
Demostración: Sólo demostraremos 3), dejando al
lector el resto, como ejercicio.
Como a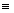 b
(mod m), se tiene que m | (b-a), es decir b-a
= mk (*)
b
(mod m), se tiene que m | (b-a), es decir b-a
= mk (*)
Análogamente como b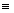 c (mod m) tenemos que m | (c-b),
es decir c-b = mp (**)
c (mod m) tenemos que m | (c-b),
es decir c-b = mp (**)
Sumando (*) y (**) tenemos que c-a = (b-a) + (c-b) = mk -
mp = mh
lo cual significa que a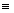 c (mod m).
c (mod m).
Es de esperarse, en vista del teorema anterior, que las
congruencias se comporten en muchos aspectos como igualdades.
Esta semejanza queda ilustrada en el siguiente teorema:
Teorema: Sean a, b, c enteros y m entero
positivo.
- Si a
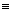 b
(mod m) entonces:
b
(mod m) entonces:
- a) a+x
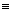 b+x (mod m) para todo
entero x.
b+x (mod m) para todo
entero x.b) ax  bx (mod m) para
todo entero x
bx (mod m) para
todo entero x
Si a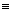 b
(mod m) y c
b
(mod m) y c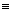 d (mod m), entonces:
d (mod m), entonces:
a) a+c 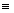 b+d (mod m)
b+d (mod m)
b) a-c  b-c (mod m)
b-c (mod m)
c) ac  bd (mod m)
bd (mod m)
d) an  bn (mod m)
para todo entero positivo n
bn (mod m)
para todo entero positivo n
Demostración: 1. Es inmediata y se deja como
ejercicio al lector, así como 2 a) y 2 b).
Para la demostración de 2 c) procedemos aplicando 1 b) y la
propiedad 3 del teorema anterior.
Si a b
(mod m) entonces ac
b
(mod m) entonces ac bc (mod m)
bc (mod m)
Si c d
(mod m) entonces bc
d
(mod m) entonces bc bd (mod m)
bd (mod m)
y en consecuencia ac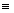 bd (mod m).
bd (mod m).
Problema 3. (Regla
de la divisibilidad entre 9)
Demuestre que un entero N, expresado en notación decimal, es
divisible entre 9 si y sólo si la suma de sus dígitos es
divisible entre 9.
Solución: sea N = a0 a1 a2
... an-1 an
N = anx100 + an-1 x101
+ an-2x102 x ... x a1x10n-1
+ a0 x10n
Como
100 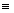 1
(mod 9) Þ anx100
1
(mod 9) Þ anx100
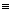 an (mod
9)
an (mod
9)
101 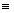 1
(mod 9) Þ an-1x101
1
(mod 9) Þ an-1x101
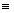 an-1
(mod 9)
an-1
(mod 9)
102 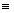 1
(mod 9) Þ an-2x102
1
(mod 9) Þ an-2x102
 an-2
(mod 9)
an-2
(mod 9)
. .
. .
. .
10n-1 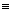 1
(mod 9) Þ a1x10n-1
1
(mod 9) Þ a1x10n-1
 a1 (mod
9)
a1 (mod
9)
10n  1 (mod 9) Þ a0 x10n
1 (mod 9) Þ a0 x10n
 a0
(mod 9)
a0
(mod 9)
Sumando término a término, obtenemos: N  a0 + a1
+ a2 + ... + an-1 + an
(mod 9)
a0 + a1
+ a2 + ... + an-1 + an
(mod 9)
Lo cual significa que 9 | N Û 9
| (a0 + a1 + a2 + ... + an-1
+ an)
Problema 4 . (Regla de
la divisibilidad entre 3)
Demuestre que un entero N, expresado en notación decimal, es
divisible entre 3 si y sólo si la suma de sus dígitos es
divisible entre 3.
Solución: Se deja al lector
Problema 5. (Otra regla
de la divisibilidad entre 3)
Demuestre que un entero N = abcd de cuatro cifras,
expresado en notación decimal, es divisible entre 9 si y sólo
si a-2b+4c+d divisible entre 9.
Solución: Se deja al lector
Teorema 3. Si ca cb (mod m) y (c,m) = d,
de modo que m = dw, entonces a
cb (mod m) y (c,m) = d,
de modo que m = dw, entonces a b (mod w).
b (mod w).
Demostración. c = dv y m = dw donde (v,w) = 1.
dw | c(a-b) y por lo tanto w | v(a-b) y como (v,w)
= 1 se tiene que w | (a-b),
es decir a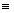 b
(mod w).
b
(mod w).
Como un caso particular tenemos el siguiente resultado:
Corolario: Si ca cb (mod m) y (c,m) = 1,
entonces a
cb (mod m) y (c,m) = 1,
entonces a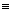 b
(mod m)
b
(mod m)
A continuación enunciaremos sin demostración un importante
resultado de la teoría de los números, conocido como:
Teorema de Fermat. Si p es primo y no divide al
entero a, entonces ap-1
 1 (mod p).
1 (mod p).
Problema 6. Demuestre
que si (n,7) = 1 entonces 7 | (n12
– 1)
Solución: Obsérvese que no podemos aplicar
directamente el teorema de Fermat pues
n13-1  1
(mod13) y lo que queremos es congruencia módulo 7.
1
(mod13) y lo que queremos es congruencia módulo 7.
Si (n,7) = 1 , entonces 7 no divide al entero n , y por el
teorema de Fermat n7-1  1 (mod7)
1 (mod7)
Es decir n6  1 (mod7). Si elevamos al cuadrado en ambos
miembros de la congruencia, tendremos que (n6 )2
1 (mod7). Si elevamos al cuadrado en ambos
miembros de la congruencia, tendremos que (n6 )2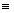 (1)2
(mod7), es decir n12
(1)2
(mod7), es decir n12 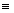 1 (mod7), lo cual significa que
7 | (n12 – 1).
1 (mod7), lo cual significa que
7 | (n12 – 1).
Problema 7. Determine
para que enteros positivos n, 2n –1
es divisible por 7.
Solución: Si n = 3k por lo siguiente:
a) Si n = 3k Þ 2n = (23)k
= 8k  1k
1k
 1 (mod 7)
Þ 7 | (2n – 1)
1 (mod 7)
Þ 7 | (2n – 1)
b) n = 3k + 1 Þ 2n = (23
)k (2) = 8k (2) 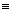 2 (mod 7)
2 (mod 7)
c) n = 3k + 2 Þ 2n 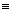 4 (mod 7)
4 (mod 7)
Problema 8. Pruebe que 2n
+ 1 nunca es divisible por 7.
Solución: Del ejercicio anterior se observa que para
cualquier entero n, 2n  1 ó 2 ó 4 (mod 7) y por lo
tanto 2n no es congruente con –1 módulo 7 y como
–1
1 ó 2 ó 4 (mod 7) y por lo
tanto 2n no es congruente con –1 módulo 7 y como
–1  6 (mod 7),
6 (mod 7),
2n no es congruente con 6 módulo 7 y en
consecuencia 2n +1 no podrá ser congruente con 7
módulo 7.
Problema 9. Demuestre
que si 7 no es un divisor de n, entonces n6
 1996 (mod 7).
1996 (mod 7).
Solución: Por el teorema de Fermat, n6  1 (mod 7), y
1
1 (mod 7), y
1 1996 (mod 7)
1996 (mod 7)
Problema 10. Demuestre
que para todo entero no negativo n, 17 es un divisor de
34n+2 + 26n+3.
Solución: Para n = 0 se cumple que 32 + 23
= 17 lo cual significa que 32 + 23  0 (mod17)
0 (mod17)
es decir 32  -23 (mod17). Si elevamos a la
potencia impar 2n + 1, obtendremos
-23 (mod17). Si elevamos a la
potencia impar 2n + 1, obtendremos
(32 )2n+1  (-23 )2n+1(mod17)
(-23 )2n+1(mod17)
34n+2  -26n+3 (mod17)
-26n+3 (mod17)
34n+2 + 26n+3  0 (mod17)
0 (mod17)
lo cual significa que 17 es un divisor de 34n+2 + 26n+3.
Problema 11. ( Olimpiada Nacional )
Demuestre que para todo entero no negativo n, se
cumple que
(n3-n)( 58n+4
+ 34n+2) es múltiplo de 3804.
Solución: Como n3-n = (n - 1)(n)(n + 1), es
múltiplo de 6 y el número 58n+4 + 34n+2
es par, por ser suma de impares, y 3804 = sólo restaría probar
que 317 | (58n+4 + 34n+2), lo
cual es completamente análogo al ejercicio No. 6 y se deja como
ejercicio al lector.
Problema 12. Encuentre
un número que al dividirse por 10 deja residuo 10, al dividirse
por 9 deja residuo 8 y así sucesivamente hasta que al dividirse
por dos deje residuo 1.
Solución: Tal número N debe cumplir lo siguiente:
N 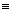 9 (mod10)
pero como 9
9 (mod10)
pero como 9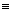 -1 (mod10)
Þ N
-1 (mod10)
Þ N  -1 (mod10)
-1 (mod10)
N 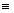 8 (mod9)
"
" 8
8 (mod9)
"
" 8 -1 (mod9) Þ N
-1 (mod9) Þ N  -1 (mod9)
-1 (mod9)
N  7 (mod8)
"
" 7
7 (mod8)
"
" 7 -1 (mod8) Þ N
-1 (mod8) Þ N  -1 (mod8)
-1 (mod8)
. . .
. . .
. . .
N  1 (mod2)
"
" 1
1 (mod2)
"
" 1 -1(mod2) Þ
N
-1(mod2) Þ
N 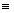 -1 (mod2)
-1 (mod2)
De las últimas congruencias a satisfacerse por N tenemos que
:
N+1 debe ser múltiplo de 2,3,4,5,6,7,8,9 y 10, siendo el
menor de esos números
N+1 = (10)(9)(4)(7) = 2520 y por lo tanto el número buscado
es N = 2519.
Problema 13. ( Olimpiada
Internacional ) Encontrar el número natural N más
pequeño que cumple las siguientes condiciones:
- En la representación decimal, termina en 6.
- Si el 6 es trasladado al principio del número, el
resultado es 4N.
Solución: Al número N lo podemos expresar de la forma
N = 10y + 6 por ejemplo abc6 = (abc)(10) + 6
6(10m) + y = 4(10y + 6) " " " 6abc =
6(103) + abc = 4(abc0) + 6
6(10m) –24 = 39y
Lo cual significa que 6(10m)  24 (mod 39).
24 (mod 39).
Es decir al dividir 600...0 ( m ceros) deja residuo 39, y tal
número es 600,000
En consecuencia N = 153,846.
Problema 14. ( Olimpiada
Nacional ) Una oficina de Turismo va a realizar una
encuesta sobre número de días soleados y número de días
lluviosos que se dan en el año. Para ello recurre a seis
regiones que le transmiten los datos de la siguiente tabla:
| Región |
Soleados o lluviosos |
Inclasificables |
| A |
336 |
29 |
| B |
321 |
44 |
| C |
335 |
30 |
| D |
343 |
22 |
| E |
329 |
36 |
| F |
330 |
35 |
La persona encargada de la encuesta no es imparcial y tiene
esos datos más detallados. Se da cuenta de que, prescindiendo de
una de las regiones, la observación da un número de días
lluviosos que es la tercera parte del de días soleados. Razonar
cuál es la región de la que prescindirá.
Solución:
Al suprimir una región, la suma de días soleados o lluviosos
de las restantes ha de ser múltiplo de 4. Las seis regiones
suman 1994 que dividido entre 4 da resto 2. El único dato de
esta columna que da resto 2 al dividirlo entre 4 es 330
correspondiente a la región F.
En términos de congruencias tenemos que:
336 0 (mod 4)
0 (mod 4)
321 1 (mod 4)
1 (mod 4)
335 3 (mod 4)
3 (mod 4)
343 3 (mod 4)
3 (mod 4)
329 1 (mod 4)
1 (mod 4)
330 2 (mod 4)
2 (mod 4)
________________________
1994 10 (mod 4)
10 (mod 4)
pero como 10 2
(mod 4), tenemos que 1994
2
(mod 4), tenemos que 1994 2 (mod 4).
2 (mod 4).
Si omitimos 330, obtendremos una cantidad congruente con 0 ,
lo cual significa que deja residuo 0 al dividirla entre 4.
A la congruencia 1994 2 (mod 4) , le restamos la congruiencia
330
2 (mod 4) , le restamos la congruiencia
330 2 (mod 4),
obteniendo
2 (mod 4),
obteniendo
1664 0 (mod 4)
0 (mod 4)
En consecuencia, suprimiendo esta región (F) quedan entre las
cinco restantes 416 días lluviosos y (3)(416) = 1248 días
soleados.
Problema 15. Demuestre
que si a es primo con 240 entonces 240 es un
divisor de a4 - 1.
Solución: La factorización de 240 en primos es:
240 = (24)(3)(5)
Así pues, debemos probar que 24 | a4 –
1, 3 | a4 – 1, 5 | a4 –
1
Claramente, por el teorema de fermat, 3 | a4 –
1 y 5 | a4 – 1
Como (a, 240) = 1 y 2 es un factor de 240, 2 no puede
ser un factor de a y en consecuencia
a= 2k + 1 Þ a2
= 4k2 + 4k + 1 es decir a2 – 1
= 4k(k + 1) y como k(k + 1) es par Þ
8 | a2 – 1.
Por otro lado como a es impar, a2 también es impar
y por lo tanto a2 +1 es par
8 | a2 – 1 y 2 | a2 –
1 Þ 24 | a4 –
1.
Problema 16. ( Concurso
Estatal ) Sean x, y , z números enteros tales que x3
+y3 - z3 es múltiplo de 7. Demuestre que
uno de ellos es múltiplo de 7.
Solución: Todo número es de alguna de las siguientes
formas: 7k, 7k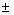 1, 7k
1, 7k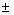 2, 7k
2, 7k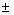 3 y como:
3 y como:
(7k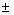 1)3
= (7k)3 + … +(
1)3
= (7k)3 + … +( 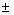 1)3
1)3
(7k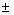 2)3
= (7k)3 + … +(
2)3
= (7k)3 + … +( 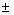 2)3 = [(7k)3 + …
2)3 = [(7k)3 + … 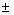 7]
7] 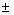 1
1
(7k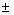 3)3
= (7k)3 + … +(
3)3
= (7k)3 + … +( 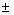 3)3 = [(7k)3 + …
3)3 = [(7k)3 + … 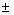 28]
28] 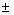 1
1
se tiene que los residuos posibles al dividir entre 7 el cubo
de un número son 0, 1, ó -1.
Si por el contrario se tiene que ninguno es múltiplo de 7,
entonces
x3 
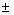 1 (mod
7)
1 (mod
7)
y3 
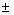 1 (mod
7)
1 (mod
7)
z3 
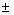 1 (mod
7)
1 (mod
7)
Por lo tanto x3 +y3 - z3
nunca podrá ser congruente con 0 módulo 7, pues con ninguna
combinación en la suma de tres números del conjunto {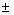 } se puede tener suma
igual a 0.
} se puede tener suma
igual a 0.
Problema 17. ( Concurso Nacional )
Pruebe que nn-1 -1 es divisible por (n-1)2
para todo entero n > 1.
Solución:
nn-1 -1 = (n-1) (nn-2 + nn-3
+ … + n + 1)
Como n  1 (mod n-1),
se tiene que nk
1 (mod n-1),
se tiene que nk  1 (mod n-1), para todo entero positivo k.
1 (mod n-1), para todo entero positivo k.
Así (nn-2 + nn-3 + … + n + 1)  1 + 1 + … + 1
1 + 1 + … + 1  n-1 (mod n-1)
n-1 (mod n-1)
y por lo tanto, (n-1)2 divide a nn-1 -1.
Problema 18. Justifique,
utilizando congruencias, el procedimiento descrito a
continuación para adivinar un número.
Diga a alguien que seleccione un número entero menor que
1000, que lo divida entre 7, 11 y 13 y proporcione los tres
residuos de la división. Usted podrá entonces decirle que
número seleccionó originalmente. Esto se hace multiplicando los
tres residuos respectivamente por los "números
mágicos" 715, 364 y 924, sumando los productos resultantes
y restando de la suma el mayor múltiplo de 1001 que deje una
diferencia positiva. Esta diferencia es el número
seleccionado.
Ejemplo: Si el número en cuestión es 523, los residuos son
5,6 y 3 respectivamente y usted escribiría:
715*15 = 3575
364*6 = 2184
924*3 = 2772
8531
El múltiplo de 1001 más cercano menor que 8531 es el 8008 y
al restarlos obtenemos 523.
Solución: Sea x el número
desconocido seleccionado, a, b y c los respectivos residuos
cuando x es dividido entre 7, 11 y 13 respectivamente, entonces:
x a (mod 7)
y 715x
a (mod 7)
y 715x (715)a
(mod 7)
(715)a
(mod 7)
x b (mod 11)
y 364x
b (mod 11)
y 364x (364)b (mod 11)
(364)b (mod 11)
x c (mod 13)
y 924x
c (mod 13)
y 924x (924)a (mod 13)
(924)a (mod 13)
restando de ambos miembros de cada congruencia, tenemos
715(x-a) 0 (mod 7)
(1)
0 (mod 7)
(1) 364(x-b) 0 (mod 11)
(2)
0 (mod 11)
(2)
924(x-c) 0 (mod 13)
(3)
0 (mod 13)
(3)
Como la congruencia (1) es divisible por 11 y 13 y en
consecuencia por 11, 13 y 7, ó por 1001 (1001 = 7*11*13).
Análogamente las congruencias (2) y (3) también son
divisibles por 1001 y sumando, tendremos
2003x - (715a +364b + 924c)  0 (mod 1001)
0 (mod 1001)
ó equivalentemente
2003x  715a +364b + 924c (mod 1001)
715a +364b + 924c (mod 1001)
pero como
2003x  x (mod 1001)
x (mod 1001)
tenemos que
x  715a +364b + 924c (mod 1001)
715a +364b + 924c (mod 1001)
Así pues, como pedimos que x < 1000, x dejará residuo x
al dividirse entre 1001 y
715a +364b + 924c también dejará residuo x al dividirse
entre 1001.
B I B L I O G
R A F Í A
1. Olimpiadas de Matemáticas: 140 Problemas, seis años de
éxitos.
Varios autores
Academia de la Investigación Científica 1993
2. Recreations in The Theory of Numbers, The Queen of
Mathematics Entertains.
Autor: Albert H. Beiler
- Dover Publications, Inc, New York 1966
3. Folletos de Problemas para las Olimpiadas
Mexicanas de Matemáticas.
Varios autores
- Sociedad Matemática Mexicana- Academia de la
Investigación Científica.
4. Problemario hacia la XI Olimpiada Mexicana de
Matemáticas, Sonora 1997.
Autores:
Enrique Hugues Galindo
Miguel Angel Moreno Núñez
Eduardo Tellechea Armenta.
- Universidad de Sonora, Marzo de 1997.
5. Soluciones al Problemario hacia la XI Olimpiada
Mexicana de Matemáticas.
Autores.
Enrique Hugues Galindo
Miguel Angel Moreno Núñez
Carlos Alberto Robles Corbalá
Eduardo Tellechea Armenta.
Universidad de Sonora, Abril de 1998.