Problema 1. Exprese el volumen de una caja sin tapa de base cuadrada , si para su construcción se emplean 8 m2 de lámina.
Solución:
x 
x
En términos de x, y el volumen de la caja es: V = x2 y.
Sin embargo como deben emplearse 8 m2 de lámina para construirla, sabemos que:
El área de la base + las cuatro caras laterales = 8m2
Es decir, en términos de x, y tendremos que x2 + 4xy = 8
Despejando y, obtenemos ![]()
Sustituyendo y en la expresión de V: ![]()
Es decir ![]()
Problema 2. Exprese el volumen de un cilindro de altura igual al triple del radio, en términos del radio.
Solución.
H = altura = 3R
R = radio
El volumen de un cilindro esta dado por V = p R2 H
Como H = 3R V = p R2 (3R)
Es decir V(R) = 3p R3
Problema 3. Exprese como función del radio, el volumen del cilindro circular recto que se puede inscribir en un cono de 12 cm de altura y 4 cm de radio de la base, de manera que los ejes del cilindro y del cono coincidan.
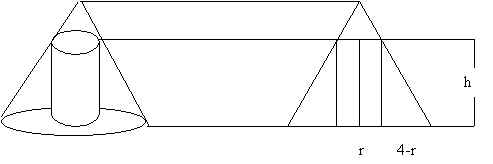
Denotemos por h la altura del cilindro y r el radio del mismo.
Mediante los triángulos semejantes de la figura de la derecha, que representa una sección transversal del cono y del cilindro, vemos que:
![]() o bien h = 3( 4 - r )
o bien h = 3( 4 - r )
Por lo tanto sustituyendo en V = p r2 h = p r2 (12 - 3r), expresamos a V en términos de x:
V = 3 p r2 (4 - r)
Regresar a la segunda lista de ejercicios
Regresar a la página principal
RESOLVIENDO PROBLEMAS DE OPTIMIZACIÓN
Problema 4. Una carretera que va de norte a sur y otra que va de este a oeste se cruzan en un punto P. Un vehículo que viaja hacia el este a 20 km/h, pasa por P a las 10 A.M. En ese mismo momento un automóvil que viaja hacia el sur a 50 km/h se encuentra2km. Al norte de P. Calcular cuándo se encuentran los dos vehículos más cerca uno del otro y cuál es la distancia mínima entre ellos.
Solución:

Al tiempo t (horas) después de las 10 A.M. el más lento se encuentra 20t km. Al este de P y el más veloz se halla 50t km al sur de la posición inicial (10 A.M.) y por lo tanto su distancia a P es (2 - 50t) km. Por el Teorema de Pitágoras, la distancia entre los dos autos en el tiempo t es:
![]()
Desarrollando obtenemos:
![]()
Claramente D alcanza su valor mínimo cuando la expresión dentro del radical es mínima, es decir tenemos que encontrar el mínimo de:
f(t) = 2900t2 - 200t +4
Como f(x) representa una parábola que se abre hacia arriba, expresémosla en la forma
f(x) = a ( x - h)2 + k
y entonces el mínimo valor se alcanzará en el vértice (h,k) de la parábola ya que a= 2900>1
Completando trinomio cuadrado perfecto:
f(t) = 2900t2 - 200t +4 = 2900 (t2 -
![]() +
+
![]() )
= 2900 (t2 -
)
= 2900 (t2 - ![]() +
+ ![]() +
+ ![]() -
- ![]() ) =
) =
= 2900 (t2 - ![]() +
+ ![]() +
0.00019) = 2900 [(t - 1/29)2 + 0.00019 ) = 2900(t
- 1/29)2 + 0.551
+
0.00019) = 2900 [(t - 1/29)2 + 0.00019 ) = 2900(t
- 1/29)2 + 0.551
f(t) = 2900(t - 1/29)2 + 0.551
f(t) representa una parábola con vértice en el punto
(1/29 , 0.551) que se abre hacia arriba, por lo que su valor
mínimo se alcanza en el punto t = 1/29 hr = 2.07 minutos, es
decir a las 10 horas con 2.07 minutos los autos se encuentran
a la mínima distancia y el valor de esa distancia mínima es
![]()
Problema 5. Una pieza larga y rectangular de lámina de 20 m de ancho va a convertirse en un canal para agua doblando hacia arriba dos de sus lados hasta formar ángulos rectos con la base. Encuentre el ancho de las partes a doblar para que el flujo del canal sea máximo.
Solución.

x 20-2x x
El flujo será máximo cuando el área de la sección transversal de la figura de la derecha sea máxima.
Expresemos pues el área en términos de x.
A = (20 - 2x) x ó bien A(x) = -2x2 + 20x
Como A(x) representa una parábola invertida, expresémosla en la forma
A(x) = a ( x - h)2 + k
y entonces el máximo valor se alcanzará en el vértice (h,k) de la parábola ya que a = -2 < 1
Completando trinomio cuadrado perfecto:
A(x) = -2x2 + 20x = -2(x2 - 10x) = -2(x2 - 10x + 25 - 25) = -2[(x-5)2 - 25]
Así pues A(x) = -2(x-5)2 + 50
y en consecuencia el máximo valor se alcanza cuando x = 5, es decir tenemos que doblar 5 metros de cada lado para que el flujo sea máximo.