|
|
|||||
 |
||||||
Diseño de situaciones Didácticas para la enseñanza del Cálculo, usando Winplot (*)
Eduardo Tellechea Armenta
Octubre 25 de 2001
Indice
Construyendo las gráficas de las funciones seno y tangente
Graficando la inversa de la función y = tan(x)
La función derivada de y = sen(x)
Software
gratuito disponible en:
http://math.exeter.edu/rparris/winplot.html
Diseño
de situaciones didácticas para la enseñanza
del
Cálculo, usando Winplot
Resumen.
El
objetivo de esta plática es el de compartir algunas experiencias, con el
uso del software dinámico Winplot,
en el curso de Cálculo Diferencial. Este software tiene la ventaja de ser
gratuito y están disponibles en la red actualizaciones periódicas – cada dos
meses aproximadamente – lo cual permite que sin problemas cada alumno pueda
tener una copia y realizar sus actividades fuera de clase.
Se
hace la aclaración de que estas actividades están contempladas como
herramientas de apoyo en el curso tradicional, no se pretende, por lo pronto,
formen parte de un curso impartido en una sala de cómputo, ya que esto, a nivel
general, no es posible en el Departamento de Matemáticas por falta de
infraestructura en equipo.
Primeramente veremos dos situaciones que generalmente se hacen en el salón de clases con todas las limitaciones que tiene el uso de gis y borrador. Posteriormente abordaremos otras situaciones en las que por medio de la visualización de la situación descubriremos algunos resultados importantes La ayuda de un software dinámico nos permite ofrecerle al alumno la posibilidad de visualizar más allá de su imaginación.
· La primera de ellas es la graficación de la función trigonométrica seno de x, la cual es la primera función “difícil” de graficársela al estudiante y generalmente se le remite a verla en algún libro, terminando el alumno por familiarizarse con ella. Winplot nos permitirá construir esta gráfica transitando del plano de la Trigonometría (matemática elemental) al del Cálculo (matemática avanzada).
· En la segunda actividad, revisaremos la definición de función inversa y a partir de una importante representación geométrica, le pediremos a Winplot que nos trace la gráfica de arco tangente como la inversa de la función tangente.
· En la tercera actividad, analizaremos una situación en la que el alumno descubrirá que la derivada de la función seno es la función coseno.
· En la cuarta actividad, “resolveremos” gráficamente el problema de encontrar una función igual a su derivada, hecho importante en el diseño de métodos para resolver ecuaciones diferenciales.
·
Finalmente
en la quinta actividad, analizaremos un problema clásico de máximos y mínimos,
para el cual Winplot nos permite visualizar en una misma pantalla, tres formas
distintas de representación del problema – Numérica, gráfica y real -.
Construyendo
las gráficas de las funciones Seno y Tangente.
Con el uso de Winplot, trazaremos
la gráfica de la función y
= sen(x), partiendo del círculo unitario.
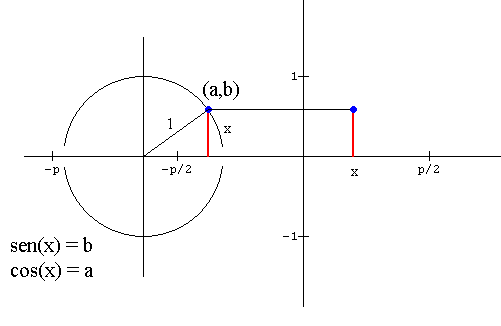
En la figura, por definición, el seno del
arco x está representado por el segmento rojo, que si lo trasladamos al sistema
cartesiano y hacemos variar x sobre la recta real, (el punto azul de la
izquierda, se moverá sobre el círculo unitario) el punto azul de la derecha,
describirá la gráfica de la función y =
sen(x).
Trigonometría
Cálculo
A continuación abriremos el archivo grafseno.wp2, en el cual veremos el trazo de la
gráfica, mediante la animación del parámetro a, el cual representa a la
variable x.
Análogamente, podemos utilizar Winplot para dibujar la gráfica de la función y = tan(x).
Graficando
la inversa de la función f(x)
= tan(x).
Obsérvese que si f(a) = b, entonces f -1(b) = a, es decir si el
punto (a, b) se
encuentra en la gráfica de f, entonces el punto (b, a) está en la
gráfica de f –1.
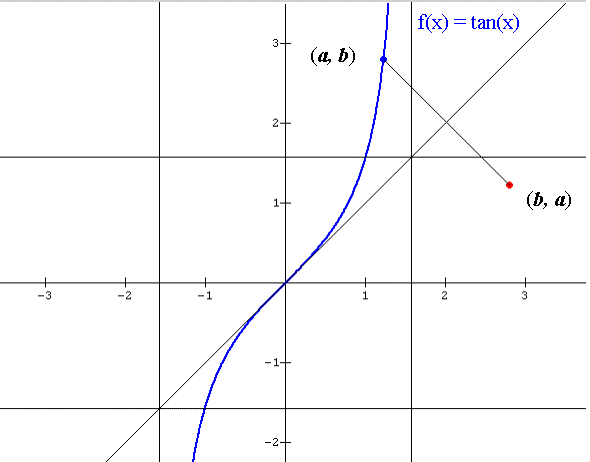
Es fácil comprobar que los puntos (a, b)
y (b, a) son simétricos con respecto a la recta
y = x, pues el
segmento que los une tiene pendiente –1 y su punto medio se encuentra sobre la
recta.
De nuevo le pedimos a Winplot que nos grafique la función inversa de y = tan(x),
manteniendo el punto rojo simétrico al punto azul, obteniendo en este trazo, la
gráfica de la función arctan(x).
La
función derivada de y = sen(x).
En esta actividad, y haciendo animación en dos
parámetros, graficaremos la función derivada de la función y = sen(x)
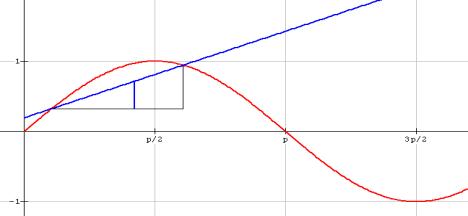
El parámetro a, representa el punto x donde queremos encontrar f ’(x) y el parámetro b, representa el incremento h, para el cálculo de la pendiente de la secante. Nótese que cuando hagamos tender b a cero, la recta secante se parece cada vez más a la recta tangente en x.
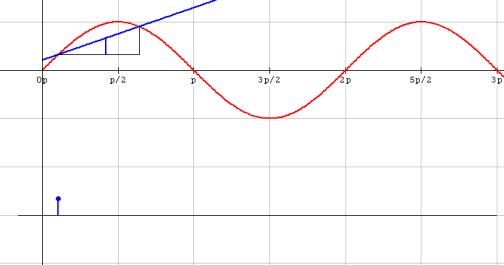
El segmento vertical azul representa la pendiente de la secante en el punto x. Si, como se muestra en la siguiente gráfica, tomamos este segmento como altura en el punto x, el extremo (punto azul), describirá la grafica de la función “pendiente” (de las secantes)
Por supuesto que cuando la recta sea tangente, el
extremo del segmento trazará la gráfica de función f ’(x) al correr
el parámetro a.
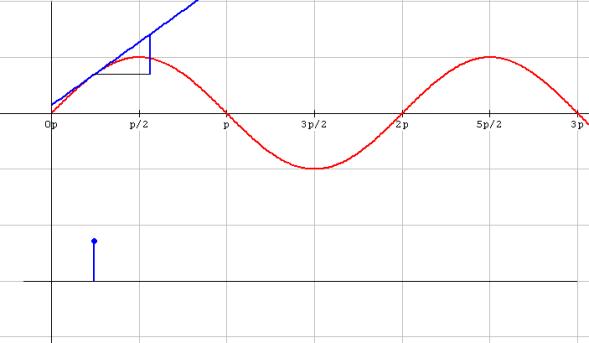
Veamos la siguiente animación que nos grafica la derivada de la función seno
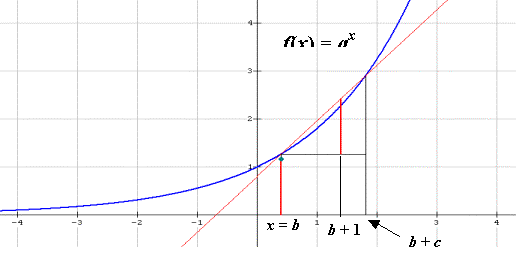
Partamos de las gráfica de f(x) = ax y su
derivada. Sabemos que la derivada de esta función es “parecida” a su
derivada..
En esta actividad, a es el parámetro que
representa la base de la función exponencial, b es el punto x
donde queremos la derivada y c representa el incremento en el cálculo de
las pendientes de las secantes.
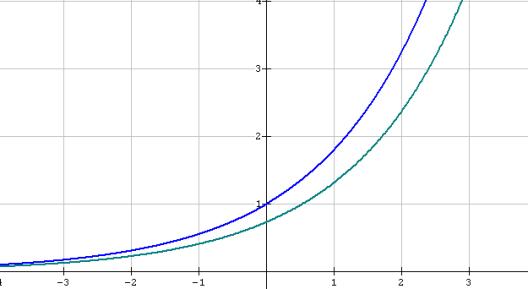Primeramente, hacemos tender
c a cero para obtener la gráfica de la derivada en cada punto x.
Después hacemos varia el parámetro b para que el punto verde, en el extremo del
segmento rojo, trace la gráfica de la derivada, obteniendo algo como lo que se
ve en la siguiente figura:
f(x) f’(x)
La gráfica de color verde corresponde a la derivada de la función f(x) = ax , de tal manera que podemos tratar de determinar el parámetro a (la base de la exponencial) para el cual ambas gráficas coinciden.
En esta actividad analizaremos un problema de máximos y mínimos en el que Winplot nos permite tener en una misma pantalla varias representaciones del mismo problema:
Diseño físico
Modelo Matemático
Exploración numérica.