OLIMPIADA SONORENSE DE MATEMATICAS 1999

Examen Selectivo

1. En un concurso escolar participan 240 estudiantes de los siguientes lugares: Hermosillo, Guaymas, Cd. Obregón y Navojoa. El número de participantes de Hermosillo es el 50% del número de estudiantes de Guaymas y 1/3 del de Cd. Obregón. El número de estudiantes de Cd. Obregón es el 75% del número de estudiantes de Navojoa. ¿Cuántos participantes de cada ciudad hay en el concurso?

2. Utilizando exclusivamente los dígitos 2 y a, se forma el siguiente número de 90 cifras:

2a22a222a2222a ... 222...2a

Si este número de 90 cifras es múltiplo de 9, obtener todos los valores posibles del dígito a.

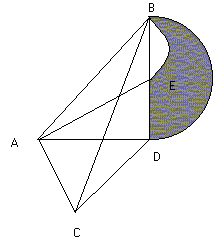
3. En la figura, AB es paralelo a CD, el triángulo ABC tiene área igual a 100 cm² . AD y BD son perpendiculares, BE = ED, los arcos BE y BD son semicircunferencias. AD mide 12.5 cm. ¿Cuál es el área de la figura sombreada?

4. Un Juego consiste en un tablero electrónico de 4x4 posiciones. En el tablero se van a colocar 16 fichas electrónicas, 8 tipo A y 8 tipo B, de tal manera que la alarma de "éxito" se acciona sólo si se llenan las dos diagonales mayores del tablero con fichas tipo B. ¿De cuántas formas distintas se pueden acomodar las 16 fichas, de tal modo que la alarma se accione?.

5. Sean a,b y c números reales no nulos (con suma no nula ) tales que:

Pruebe que también se verifica:

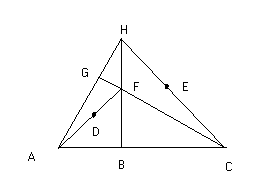
En la figura se tiene que: AC y HB son perpendiculares, AB = BF y BC = BH. D es el punto medio de AF y E es el punto medio de CH. AF = x y CH = y. ¿Cuánto mide GD? ¿Cuánto mide GE?