Si una variable independiente
Similarmente, cuando
Consideramos la función
El símbolo
![]() se lee
infinito, es de carácter posicional, no representa ningún número real.
se lee
infinito, es de carácter posicional, no representa ningún número real.
Si una variable independiente
![]() está creciendo
indefinidamente a través de valores positivos, se escribe
está creciendo
indefinidamente a través de valores positivos, se escribe
![]() (que se lee:
(que se lee: ![]() tiende a más infinito), y si decrece a través de valores negativos, se denota
como
tiende a más infinito), y si decrece a través de valores negativos, se denota
como
![]() (que
se lee:
(que
se lee: ![]() tiende a
menos infinito).
tiende a
menos infinito).
Similarmente, cuando
![]() crece
indefinidamente y toma valores positivos cada vez mayores, se escribe
crece
indefinidamente y toma valores positivos cada vez mayores, se escribe
![]() ,
y si decrece tomando valores negativos escribimos
,
y si decrece tomando valores negativos escribimos
![]() .
.
Consideramos la función
![]() definida por
definida por
![]() para
para
![]() .
Vamos a determinar el comportamiento de la función cuando
.
Vamos a determinar el comportamiento de la función cuando
![]() cuando
cuando
![]() y cuando
y cuando
![]() .
Para ello nos ayudamos de las tablas siguientes:
.
Para ello nos ayudamos de las tablas siguientes:
| a. | 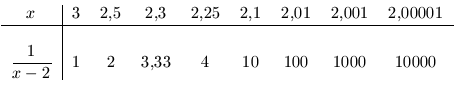 |
En este caso, cuando
![]() , la función
, la función
![]() tiende a
tomar valores positivos cada vez mayores. Esto podemos escribirlo como
tiende a
tomar valores positivos cada vez mayores. Esto podemos escribirlo como
![]() , es decir
, es decir
![]()
| b. | 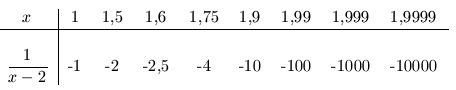 |
Ahora, cuando ![]() toma valores cercanos a 2 pero menores que 2, la función tiende a valores
negativos cada vez menores. Es decir,
toma valores cercanos a 2 pero menores que 2, la función tiende a valores
negativos cada vez menores. Es decir,
![]() cuando
cuando
![]() ,
o sea
,
o sea
![]() .
.
| c. | 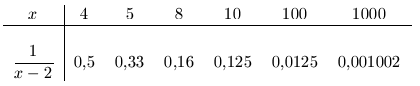 |
Ahora observe que es
![]() la que tiende a
tomar valores positivos cada vez mayores, obteniendo como resultado que
la que tiende a
tomar valores positivos cada vez mayores, obteniendo como resultado que
![]() tiende a
valores cercanos a cero.
tiende a
valores cercanos a cero.
Así
![]() ,
o sea,
,
o sea,
![]() cuando
cuando
![]() .
.
| d. | 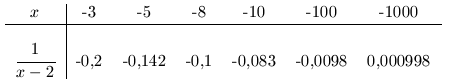 |
En forma similar a la tabla anterior se tiene que
![]() cuando
cuando
![]() es decir,
es decir,
![]()
Podemos representar gráficamente el comportamiento de la función
![]() en la forma
siguiente.
en la forma
siguiente.
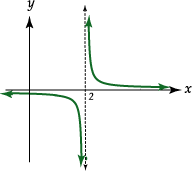
Consideramos ahora la función
![]() definida por
definida por
![]() para
para
![]() ,
cuya representación gráfica es la siguiente:
,
cuya representación gráfica es la siguiente:
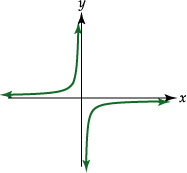
Podemos decir que:
| a. |
|
| b. |
|
Ejercicio
Determine:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
utilizando para ello la función
,
utilizando para ello la función
![]() .
.
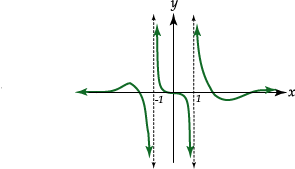
Daremos ahora algunas definiciones sobre límites infinitos, y límites al
infinito.
| Definición | |
| Se dice que
|
Gráficamente se tiene:
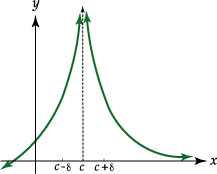
Esta definición nos dice que es posible hacer
![]() tan grande
como se quiera, (es decir, mayor que cualquier número positivo
tan grande
como se quiera, (es decir, mayor que cualquier número positivo
![]() ), tomando
), tomando
![]() suficientemente
cerca de
suficientemente
cerca de ![]() .
.
Ejemplo
Consideremos la representación gráfica de la función
![]() definida por:
definida por:
![]()

Demostremos ahora que
![]()
Para hacer la prueba, debe establecerse que dado un
![]() existe
existe
![]() tal que
tal que
![]() .
.
Observe que:
![]() .
.
Luego, dado
![]() ,
escogemos
,
escogemos
![]() de tal forma que se satisfaga que
de tal forma que se satisfaga que
![]() .
Si tomamos, por ejemplo,
.
Si tomamos, por ejemplo,
![]() cuando
cuando
![]() ,
es decir, cuando
,
es decir, cuando
![]() .
.
| Definición | |
| Se dice que
|
Gráficamente se tiene que:
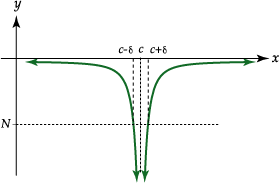
La definición anterior afirma que es posible hacer
![]() menor que
cualquier número negativo
menor que
cualquier número negativo
![]() , tomando
, tomando
![]() suficientemente
cerca de
suficientemente
cerca de ![]() .
.
Ejemplo: Consideremos la representación
gráfica de la función
![]() definida por
definida por
![]()
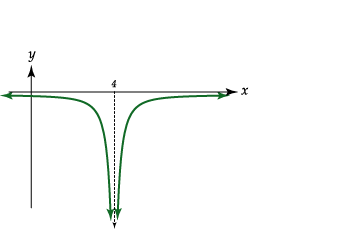
En la grafica se ve que
![]()
| Definición | |
| Se dice que
|
Similarmente, se dice que
![]() tiende a
tiende a
![]() cuando
cuando
![]() tiende a
tiende a
![]() por la
izquierda y se escribe
por la
izquierda y se escribe
![]() si
si ![]() siempre que
siempre que
![]() (Observe que
(Observe que ![]() es mayor que cero pues
es mayor que cero pues
![]() ya que
ya que
![]() ).
-El comportamiento de la función
).
-El comportamiento de la función
![]() definida por
definida por
![]() cuando
cuando
![]() ,
está regido por la definición anterior. Recuerde la representación gráfica de
esta función hecha anteriormente.
,
está regido por la definición anterior. Recuerde la representación gráfica de
esta función hecha anteriormente.
-Los símbolos
![]() y
y
![]() se definen análogamente, escribiendo
se definen análogamente, escribiendo
![]() en
vez de
en
vez de ![]() .
(note que si
.
(note que si
![]() entonces
entonces
![]() )
)
Gráficamente se tiene:
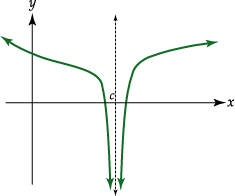
En esta representación gráfica se tiene que tanto al acercarnos
a ![]() por la
derecha como por la izquierda, los valores de la función son negativos cada vez
mayores, (mayores en el valor absoluto), es decir, se tiene que
por la
derecha como por la izquierda, los valores de la función son negativos cada vez
mayores, (mayores en el valor absoluto), es decir, se tiene que
![]() y cuando
y cuando
![]()
Podríamos representar gráficamente este comportamiento de una
función ![]() como
sigue:
como
sigue:
| Definición | |
| Se dice que
|
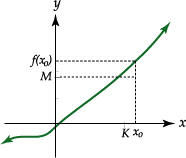
Observe que
![]() y que
y que
![]()
Podemos anotar que
![]()
Ejemplo:
Demostraremos que
![]()
Para probar este límite, se debe establecer que dado un
![]() , debe
existir
, debe
existir
![]() siempre que
siempre que
![]()
Ahora, como
![]() si y
solo si
si y
solo si
![]() ,
entonces, para cualquier número
,
entonces, para cualquier número
![]() , podemos
tomar
, podemos
tomar
![]() de
tal forma que se cumpla que
de
tal forma que se cumpla que
![]() .
.
Por ejemplo, si
![]() entonces
entonces
![]() .
Esto significa que
.
Esto significa que
![]() es
mayor a 1000 siempre que
es
mayor a 1000 siempre que
![]() sea mayor que
10.
sea mayor que
10.
La función f definida por
![]() , con
, con
![]() ,
tiene como representación gráfica la siguiente
,
tiene como representación gráfica la siguiente
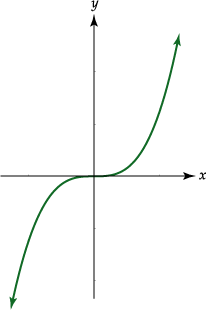
Nota: En forma similar a la
definición anterior pueden definirse
![]() ,
,
![]() y
y
![]()
En las siguientes representaciones gráficas vamos a ejemplificar
el comportamiento de una función f en el que se evidencien los límites
anteriores:
| a. |
|
|
| b. |
|
|
| c. |
|
|
Ejercicio:
En cada caso, utilizando el dibujo que se da, determine los límites que se
indican:
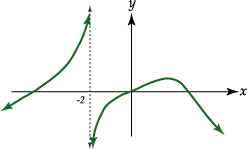
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]()
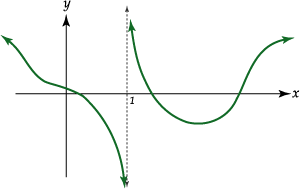
a)
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]()
Consideraremos ahora la función f definida por
![]()
En las siguientes tablas vamos a evidenciar su comportamiento cuando
![]() y cuando
y cuando
![]() :
:
| a. | 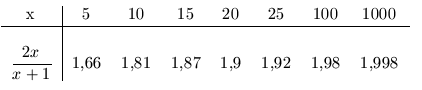
|
| b. | 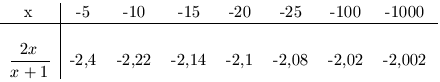
|
En ambas tablas puede observarse que cuando
![]() toma valores
positivos o valores negativos cada vez mayores, (mayores en valor absoluto), se
tiene que la función
toma valores
positivos o valores negativos cada vez mayores, (mayores en valor absoluto), se
tiene que la función
![]() tiende a
acercarse a 2, por lo que se puede escribir que:
tiende a
acercarse a 2, por lo que se puede escribir que:
![]() y
y
![]()
A continuación hacemos la respectiva representación gráfica de la función
![]() :
:
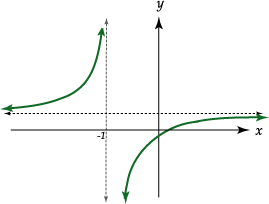
Damos ahora las definiciones para los límites cuyo resultado es
una constante cuando
![]() y cuando
y cuando
![]()
| Definición | |
| Sea
El límite de
|
Ejemplo
Probar que
![]()
Hay que demostrar que para
![]() existe
existe ![]() tal que
tal que
![]() si
si
![]()
Se tiene que
![]()
Si ![]() entonces
entonces
![]() por lo que:
por lo que:
![]()
Luego, dada
![]() se cumple que
se cumple que
![]() si y solo si
si y solo si
![]() ,
o sea, si
,
o sea, si
![]() ,
por lo que podemos tomar
,
por lo que podemos tomar
![]() de tal forma que se verifique que
de tal forma que se verifique que
![]() siempre que
siempre que
![]() .
.
Por ejemplo, si
![]() entonces
entonces ![]() por
lo que:
por
lo que:
![]()
La representación gráfica de la función es la siguiente:
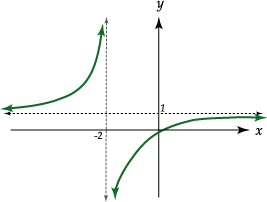
| Definición | |
| Sea
El límite de |