Valores pragmático y
epistémico del método
de eliminación de
Gauss-Jordan en ambientes CAS
Ana Gpe. Del Castillo
Bojórquez
Departamento de
Matemáticas
Universidad de Sonora
Resumen
El propósito de este trabajo es analizar el papel del
método de eliminación de Gauss-Jordan tanto como una técnica para la resolución
de Sistemas de Ecuaciones Lineales, así como un elemento de significación en la
construcción de algunos conceptos del álgebra lineal. Se pretende analizar cómo cambia el balance
entre estos dos papeles cuando se toman en consideración los sistemas de
cómputo simbólico como recurso en el aula. Asimismo, se analizan estos dos
papeles en relación con algunos comandos y aplicaciones incluidos en la
calculadora simbólica Voyage 200 de Texas Instruments que sirven también para
resolver sistemas de ecuaciones lineales. Finalmente, se presenta un programa
interactivo para la calculadora que se diseñó con la intención de rescatar el
valor epistémico del mencionado método de eliminación.
Introducción
Algunos especialistas en el campo de
Aspectos Teóricos
En este trabajo se toma en consideración
En esta teoría se asume que los objetos
matemáticos emergen y evolucionan a partir de situaciones problémicas y las
prácticas que se ponen en juego para resolverlas, ya sea de manera personal, o
en el seno de una institución. Estas prácticas, o praxeologías como las llama Chevallard, se describen en términos de
las tareas o situaciones problémicas en las cuales se involucra el objeto
matemático, de las técnicas que se emplean para resolverlas, y de una reflexión y un discurso que explique y
justifique el empleo de esas técnicas.
Así, el significado, personal o institucional,
(Godino y Batanero, 1994) de un objeto matemático se caracteriza por medio de
las praxeologías que lo ponen en juego.
Es por ello que, para analizar los procesos de
enseñanza y aprendizaje de las matemáticas, Godino propone los siguientes tipos
de entidades como elementos constitutivos del significado de los objetos
matemáticos:
- Lenguaje (términos, expresiones,
notaciones, gráficos).
- Situaciones (problemas más o menos
abiertos, aplicaciones dentro y fuera de las matemáticas, ejercicios,
etc.).
- Acciones del sujeto ante las tareas
matemáticas (operaciones, algoritmos, técnicas de cálculo, procedimientos,
estrategias, etc.).
- Conceptos, dados mediante definiciones o
descripciones.
- Propiedades o atributos de los objetos
mencionados, que suelen darse como enunciados o proposiciones.
- Argumentaciones que se usan para validar y
explicar las proposiciones.
Estos seis tipos de entidades que se ponen en
juego en la actividad matemática, son los constituyentes primarios de otros
objetos más complejos.
Las situaciones problémicas promueven y
contextualizan la actividad matemática, y junto con las acciones constituyen el
componente praxémico de las matemáticas, por lo que podemos considerarlos como
praxis. Los conceptos, propiedades y argumentaciones desempeñan un papel
normativo en las matemáticas. Son el resultado de una actividad reflexiva y
regulativa de la praxis; y constituyen el componente teórico o discursivo
(logos). El lenguaje está presente de manera intrínseca y constitutiva tanto en
la praxis como en el logos.
Podemos afirmar que a través de las prácticas,
donde el trabajo técnico juega un papel esencial, se construyen los objetos
matemáticos y las conexiones entre éstos, los cuales serán luego considerados
de naturaleza conceptual.
Una técnica es, pues, una manera de resolver
una tarea. Las técnicas no solamente tienen un valor pragmático que les permite
producir resultados, sino que tienen también un valor epistémico, puesto que forman
parte del significado de los objetos, y son también una fuente de nuevas
preguntas que contribuyen a la construcción de nuevo conocimiento.
La presencia de tecnología computacional
modifica las prácticas personales e institucionales, y cambia el balance entre
el trabajo técnico y el conceptual. Asimismo, los valores pragmático y
epistémico de las técnicas, también cambian.
Analizaremos algunas técnicas instrumentadas en
ambientes CAS, específicamente utilizando la calculadora simbólica Voyage 200,
cuando la tarea es resolver sistemas de ecuaciones lineales.
Resolviendo un SEL con
la calculadora Voyage 200
Para resolver un sistema de ecuaciones lineales
la calculadora cuenta con una serie de comandos y aplicaciones. Una técnica
instrumentada que los tome en consideración, tendrá un alto valor pragmático
puesto que permitirá obtener la solución del mismo, obviamente, considerando
las restricciones inherentes a la capacidad del dispositivo. El valor
epistémico de la técnica dependerá, como se mencionó anteriormente, de los
objetivos de la enseñanza.
Supongamos que queremos resolver el siguiente
sistema de ecuaciones lineales:
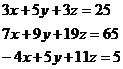
El comando solve ( ).
Para resolver el sistema simplemente se
introduce en la línea de comando de la aplicación HOME la instrucción
solve(
and 
and 
, 
)
y la calculadora dará el resultado de forma inmediata, como se muestra a continuación:
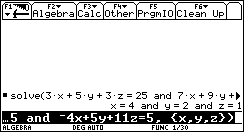
Fig. 1
Obviamente, el valor pragmático
de la técnica es elevado pues obtenemos el resultado de forma inmediata. El
valor epistémico depende de los objetivos de la enseñanza. Puede enfocarse, por
ejemplo, en entender qué significa resolver un sistema de ecuaciones lineales,
o bien, en explorar la naturaleza de la solución que puede obtenerse al tratar
de resolver varios sistemas. El comando solve( ) puede utilizarse también para
resolver sistemas de ecuaciones no lineales.
La aplicación Simultaneous
Equation Solver
Simultaneous Equation Solver es una aplicación desarrollada por Texas Instruments para la
calculadora Voyage 200, con el propósito de resolver sistemas de ecuaciones
lineales. Para resolver el sistema será necesario introducir la matriz
aumentada del sistema, por lo que podemos advertir que ésta técnica
instrumentada, además de resultar de un gran valor pragmático, contribuirá a la
construcción de los conceptos de matriz, matriz del sistema, matriz aumentada
del sistema. También puede ser utilizada para hacer una exploración de la
naturaleza de las soluciones de distintos sistemas de ecuaciones lineales. Todo
esto es considerado parte de su valor epistémico.
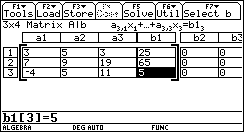
Fig. 2
Los comando ref( ) y rref(
).
El uso de los comandos ref y rref no nos dan de manera explícita la
solución del sistema de ecuaciones, por lo que su valor pragmático pudiera
verse disminuido. Estos comandos nos llevan
la forma escalonada o la forma escalonada reducida por renglones de la
matriz aumentada del sistema, por lo que el estudiante debe interpretar la
matriz en términos de un sistema equivalente al original, en el cual, la
solución podrá obtenerse de una manera sencilla, lo cual incrementa su valor
epistémico. El utilizar estos comandos involucra una serie de conceptos básicos
del álgebra lineal como matriz, matriz del sistema, matriz aumentada del
sistema, sistemas equivalentes, matriz triangular, forma escalonada o forma
escalonada reducida de una matriz,
consistencia o inconsistencia de un sistema lineal, tipos de solución de
un sistema lineal, dependencia e independencia lineal, operaciones elementales
entre renglones, etc. Sin embargo, la inmediatez de los resultados, puede
disminuir el valor epistémico de la técnica, si las operaciones elementales
entre renglones no se han trabajado lo suficiente.
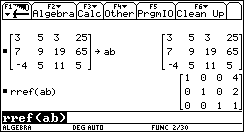
Fig. 3
El Editor de
Ecuaciones, el Editor de Gráficas y el Editor de Tablas.
Estas tres aplicaciones de la calculadora
pueden utilizarse en el caso de sistemas con dos variables. El valor pragmático
es reducido si consideramos el tiempo que se invierte para analizar la solución
del sistema en estos tres ambientes. Sin embargo el valor epistémico es elevado
pues a través de representaciones múltiples, se construye el significado de lo
que es la solución de un sistema de ecuaciones de 
y acerca de las
posibles soluciones, lo cual servirá como base para el análisis de sistemas con
más variables.
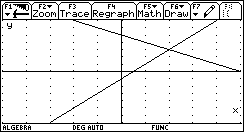
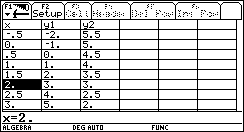
Fig. 4
El método de
eliminación de Gauss-Jordan
Implementación con
lápiz y papel
El valor pragmático del método está en el hecho
de que nos lleva sistemáticamente a la solución de cualquier sistema de
ecuaciones lineales. Sin embargo, este valor pragmático disminuye conforme
aumenta la dimensión del sistema, por la gran cantidad de operaciones que deben
realizarse. Este resulta tedioso y los errores son comunes.
En cuanto a su valor epistémico, podemos decir
que es en su implementación donde puede construirse significado para muchos
objetos matemáticos, como son:
- Conceptos
•
Transformaciones
elementales y Sistemas equivalentes
•
Matrices
y representación matricial de un SEL.
•
Vectores
renglón y vectores columna.
•
Operaciones
elementales en los renglones y formas escalonadas reducidas por renglones.
•
Combinaciones
lineales, espacios generados, subespacios, dependencia e independencia lineal,
bases, inversibilidad, determinantes, rango, etc.
•
Variables
básicas y libres.
- Propiedades
y argumentaciones
•
Permite
determinar algebraicamente que un SEL de 
o no tiene solución, o
tiene solución única, o tiene una infinidad de soluciones aun cuando la
interpretación geométrica deja de tener sentido.
•
Un
sistema homogéneo con más variables que ecuaciones tiene una infinidad de
soluciones.
Implementación en la
calculadora
El uso del comando rref(
) eleva el valor
pragmático del método de eliminación de Gauss-Jordan como técnica para la
solución de sistemas de ecuaciones lineales. Sin embargo, la manera de
presentar el resultado de forma tan inmediata, disminuye considerablemente el
valor epistémico de la técnica. Los sistemas de cómputo simbólico, en
particular la calculadora simbólica Voyage 200 tiene algunos comandos internos que
pueden ayudar a reconstruir el valor epistémico de la técnica como son:
•
RowSwap,
para intercambio de renglones
•
mRow,
para multiplicar un renglón por un número
•
mRowAdd,
para sumar a un renglón el múltiplo de otro
Fig. 5
Sin embargo, el manejarlos de manera
eficiente requiere de tiempo. En una experiencia en el aula, el manejo de los
comandos resultó ser complicado para un poco más de la mitad de un grupo de 35
estudiantes, quienes no lograron instrumentar la técnica adecuadamente. Al
aplicar una operación elemental que no arrojaba el resultado esperado, los
estudiantes estaban lejos de pensar en la operación inversa y, recuperar la
matriz anterior a esa operación exige un buen manejo de la aplicación HOME de la
calculadora. Se invertía mucho
tiempo en la operación de la calculadora y los estudiantes se perdían en el
proceso. Además, el obtener la forma escalonada reducida de la matriz se
convertía en el fin y no el medio para resolver el sistema de ecuaciones.
Es por eso que se decidió utilizar recursos de
programación para disminuir las dificultades del manejo técnico de la
calculadora por parte de los estudiantes.
El programa gaussjor(
)
El programa gaussjor() tiene como objetivo apoyar el aprendizaje del método de eliminación de Gauss-Jordan para la solución de sistemas de ecuaciones lineales. El valor pragmático del programa es reducido en cuanto a que la calculadora por si misma, como se mostró anteriormente, tiene comandos que directamente nos llevan a la forma reducida escalonada de la matriz, o bien, comandos que nos llevan directamente a la solución de un sistema de ecuaciones lineales. Sin embargo, el propósito del programa es ayudar al estudiante a construir significados en cuanto a conceptos fundamentales del álgebra lineal, los cuales se mencionaron en la sección anterior. Para tal efecto, se busca crear un ambiente amigable en el que, de manera interactiva, el estudiante pueda llevar una matriz a su forma escalonada reducida por renglones. El programa también puede ilustrar la manera de hacerlo, para aquellos estudiantes que tengan dificultades y necesiten apoyo especial en su tarea. Asimismo, el programa también incluye la opción de mostrar la forma escalonada reducida en un solo paso, si así se prefiere.
Operación del programa
El
programa gaussjor() requiere manejar una matriz, la cual puede encontrarse
guardada en la memoria de la calculadora, o puede introducirse directamente
durante la corrida del programa. Esta matriz, no puede ser de dimensiones
grandes, por las restricciones impuestas por el tamaño de la ventana de
visualización; pueden manejarse a lo más matrices de 
, aunque esto puede variar por el tamaño de las
entradas de la matriz. Sin embargo, se reitera que el uso del programa es más
didáctico que práctico. Para matrices más grandes, se pueden utilizar el Editor
de Base de Datos y Matrices y los comandos apropiados que ya vienen incluidos
en la calculadora.
Para iniciar la corrida de este programa se escribe gaussjor() en la línea de comando de la pantalla principal HOME y se presiona ENTER , como se muestra a continuación.
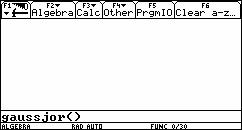
Fig. 6
Es importante verificar que el fólder donde se encuentra el programa, sea el fólder actual, para que éste pueda ejecutarse. En este caso el fólder es ALGEBRA.
A continuación aparece las siguientes pantallas que describen brevemente el propósito del programa y muestra algunos datos relativos a la elaboración del programa:
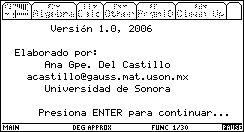
Fig. 7
Al presionar ENTER aparece la siguiente pantalla que muestra una barra de herramientas, a las que tendremos acceso mediante las teclas de función.
Fig. 8
Al presionar la tecla ƒ, se muestra un menú de opciones, a través de las cuales se selecciona el modo de operación del programa: interactivo, ilustrativo o de un solo paso. Para seleccionar la opción deseada se utilizan las teclas de navegación DFC, o bien, la tecla del número correspondiente.
Al seleccionar la opción Interactivo, Ilustrativo o Un paso, se
vuelve a la pantalla de
Fig. 9
Al presionar la tecla „, se tiene acceso a una ventana de diálogo como la que se muestra abajo, en la que debe introducirse la matriz aumentada de un SEL, o bien, una matriz, la cual se quiere llevar a su forma escalonada reducida por renglones. Debemos tener en cuenta, que la matriz no puede ser muy grande, por las restricciones de tamaño de la ventana de visualización.
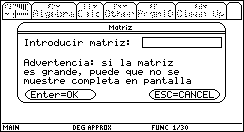
Fig. 10
Este es un punto delicado en el programa pues debe tratar de preverse cualquier situación anómala en la introducción de los datos, y tratar de controlarla para evitar la interrupción del programa. Si la matriz se encuentra previamente en la memoria de la calculadora, es posible introducir la matriz tecleando el nombre de variable en la que se encuentra almacenada. Si no es así, ésta debe teclearse entre corchetes, introduciendo renglón por renglón, los elementos de la matriz separados con comas; para indicar el cambio de renglón se utiliza punto y coma.
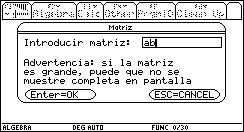
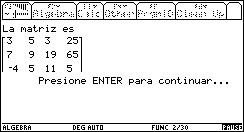
Fig. 11
Si se
presiona ESC
la matriz no se guardará y volveremos a la barra de herramientas de
Al
presionar ENTER ,
se llevará a cabo una validación de los datos introducidos. Si se teclea
erróneamente, o no se introduce una matriz, pueden aparecer los mensajes que se
muestran abajo, y al presionar ENTER
se regresa a la pantalla de
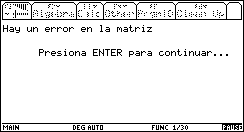
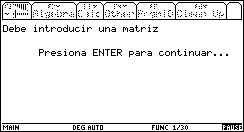
Fig. 12
Si no hay
problema, y se ha introducido correctamente una matriz, al presionar ENTER también volveremos a la barra de herramientas
de
Una vez
introducida la matriz, se puede tener acceso a la herramienta Ejecutar, la
cual es accesible mediante la tecla de función F3
En este momento, es posible tener tres acciones distintas, dependiendo del modo seleccionado.
Si el modo seleccionado es Un paso entonces, se mostrará la forma escalonada reducida por renglones de la matriz de manera inmediata.
Fig. 13
Si se ha seleccionado el modo Ilustrativo, entonces el programa muestra paso a paso el algoritmo para llevar la matriz a su forma escalonada reducida, especificando las operaciones elementales con renglones que se están efectuando. Se muestran abajo algunas pantallas del proceso.
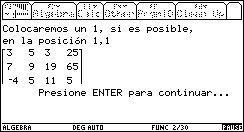
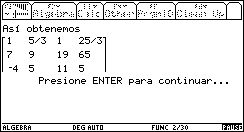
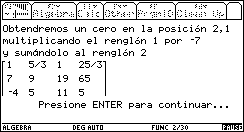
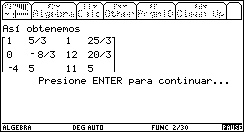
Fig. 14
etc., hasta llegar a la forma escalonada reducida por renglones.
En el modo Interactivo, el estudiante irá seleccionando las operaciones elementales en los renglones para escalonar la matriz. Para ello, se utiliza una barra de herramientas, como se muestra en la siguiente figura.
Fig. 15
Al presionar la tecla ƒ, se muestra un menú de opciones en el que se deberá seleccionar la operación elemental a llevar a cabo.
Si se selecciona Intercambio de renglones entonces aparecerá un cuadro de diálogo en el que deberán introducirse los números de renglón correspondientes. En el programa se toman las precauciones necesarias para filtrar los datos de entrada, de modo que éstos sean válidos, para cuidar el buen funcionamiento del mismo. En este caso, los números introducidos deben ser enteros positivos y deben corresponder a las dimensiones de la matriz con la que se está trabajando.
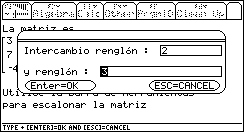
Fig. 16
En el caso de que no se introduzcan datos numéricos, o que éstos no correspondan a las dimensiones de la matriz en cuestión, aparecerán los siguientes mensajes de error.
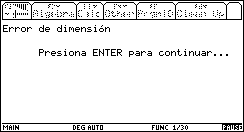
Fig. 17
Si se selecciona Mult. Renglón por número entonces aparecerá un cuadro de diálogo en el que deberán introducirse el número de renglón correspondiente y el número por el que se va a multiplicar. De nuevo, en el programa se toman las precauciones necesarias para filtrar los datos de entrada, de modo que éstos sean válidos, para cuidar el buen funcionamiento del mismo.
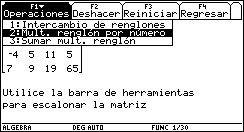
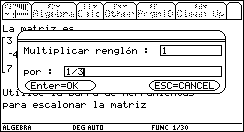
Fig. 18
Los mensajes de error para entradas no válidas, son semejantes a los del caso anterior.
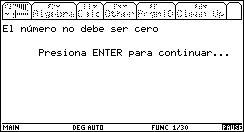
Fig. 19
Si se selecciona Sumar mult. renglón entonces aparecerá un cuadro de diálogo en el que deberán introducirse los números de renglón correspondientes y el número por el que se va a multiplicar uno de ellos para sumárselo al otro. De nuevo, en el programa se toman las precauciones necesarias para filtrar los datos de entrada, de modo que éstos sean válidos, para cuidar el buen funcionamiento del mismo.
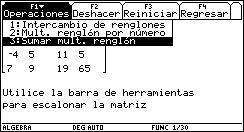
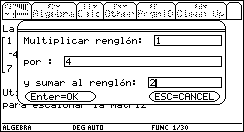
Fig. 20
Los mensajes de error para las entradas no válidas son semejantes a los mostrados en los casos ya mencionados.
En caso de efectuar una operación elemental en los renglones que no produce el efecto deseado, es posible deshacer esa operación utilizando la herramienta Deshacer, accesible a través de la tecla de función F2. Se puede deshacer sólo una operación. En caso de querer iniciar de nuevo, se tiene esa opción presionando F3.
Para
regresar a la pantalla principal, mostrada en
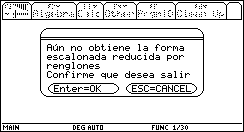
Fig. 21
Para terminar la ejecución del programa, se presiona la tecla F4 en la pantalla principal (Fig. 8)
Resultados y
Conclusiones
Al utilizar el programa gaussjor( ) como
técnica instrumentada para resolver sistemas de ecuaciones lineales, se logró
el objetivo de disminuir las dificultades en cuanto al manejo de la calculadora
y se sintió un ambiente más tranquilo en el salón de clase, lo que a su vez nos
permitió enfocarnos en los contenidos matemáticos más que en el dominio del
instrumento. En cuanto al valor epistémico de la técnica instrumentada, se
presentó un análisis de su potencial. Sin embargo, la realización efectiva de
ese potencial no depende solamente del uso del programa presentado, sino de las
situaciones abordadas, y de la reflexión y el discurso que explique y
justifique el empleo de la técnica.
Referencias
Artigue
M. (2002), Learning mathematics in a CAS
environment: the genesis of a reflection about instrumentation and the
dialectics between technical and conceptual work. CAME Forum.
Godino,
J., Batanero, C. (1994) Significado institucional y personal de los objetos
matemáticos. Recherches en Didactique des
Mathématiques, Vol. 14, No. 3,
pp. 325-355.
Guin,
D.; Ruthven, K.; Trouche, L. (eds.) (2005), The Didactical Challenge of
Symbolic Calculators: Turning a Computational Device into a Mathematical
Instrument. Series: Mathematics Education Library, Vol. 36 Springer,
Godino,
J. D. (2003). Teoría de las
funciones semióticas. Un enfoque ontológico-semiótico de la cognición e
instrucción matemática. Departamento de Didáctica de
Lay, D. (2001), Álgebra Lineal y sus Aplicaciones, 2ª. Ed., Pearson Educación
México.
Anton,
H. (2003), Introducción al Álgebra Lineal, 3ª. Ed., Limusa Wiley.
Chevallard Y. (1992). Concepts fondamentaux de la
didactique : perspectives apportées par une approche anthropologique. Recherches en Didactique des
Mathématiques,
12/1, 77-111.
Anexos
El código del programa se presenta a continuación.