EL CONCEPTO DE DIFERENCIAL
Existen muchas situaciones, dentro y fuera de las matemáticas, en que necesitamos estimar una diferencia, como por ejemplo en las aproximaciones de valores de funciones, en el cálculo de errores al efectuar mediciones (Valor real menos valor aproximado) o simplemente al calcular variaciones de la variable dependiente cuando la variable independiente varía "un poco", etc. Utilizando a la recta tangente como la mejor aproximación lineal a la función en las cercanías del punto de tangencia, aproximaremos esta DIFERENCIA con la diferencia sobre la recta tangente, a la que llamaremos EL DIFERENCIAL de la función en el punto.
DEFINICION Y EJEMPLOS
Consideremos la siguiente ilustración en donde aproximamos a la función f por su recta tangente.
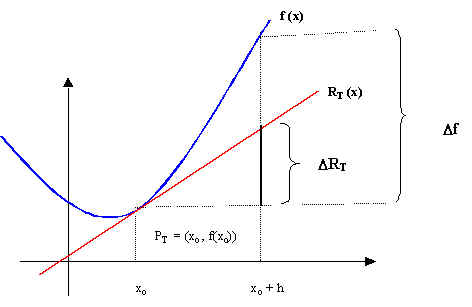
Considerando que la recta tangente es la mejor
aproximación lineal a la gráfica de f en las cercanías del
punto de tangencia PT, si le
llamamos 
a la variación de f cuando x varía de xo
a xo + h y 
a la variación de la recta tangente en
el mismo rango de variación en x, podemos afirmar que para
valores de h "cercanos" a 0, estas dos variaciones son
muy parecidas, es decir, D f
@ D RT .
Podemos expresar a D RT en términos de h y el ángulo q que forma la recta tangente con el eje de las abscisas. En el triángulo de la figura, que extraemos a continuación, se observa lo siguiente:
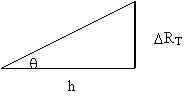
En virtud de que D RT es un aproximador de la DIFERENCIA D f, lo definiremos como EL DIFERENCIAL DE f en el punto xo, con respecto al incremento h y lo denotaremos por df, es decir,
df = f '(xo)h
Observación: El diferencial, en general depende de h y del punto xo. Por ejemplo el diferencial de f(x) = x2 es:
df = f ' (xo)h = (2xo)h
que también lo podemos expresar como:
d(x2) = (2xo)h
Si especificamos el punto xo, el diferencial dependerá únicamente de h, como se aprecia en los siguientes ejemplos:
a) El diferencial de f(x) = x2 en xo =3 es d(x2) = 6h
b) El diferencial de f(x) = x2 en xo =7 es d(x2) = 14h
c) El diferencial de f(x) = x3 en xo =2 es d(x3) = 12h
En el caso de la función identidad f(x) = x, como f '(xo) = 1 para todo xo, su diferencial nos queda como df = f '(xo)h = h o bien dx = h
Como h es el diferencial de la función identidad, podemos re-escribir el diferencial de una función f derivable en xo, como:
df = f '(xo)dx
Esta expresión nos dice que la variación de una función f es aproximadamente proporcional a la variación de su variable independiente, donde la constante de proporcionalidad es la derivada en el punto en cuestión.
En los siguientes ejemplos estimaremos la variación D f para xo y h dados y la compararemos con el diferencial.
Ejemplo . Verifique que:
a) Para f(x) = x2 se cumple que D f @ df en xo = 1 y h = 0.1
Solución:
D f = f(1.1) - f(1) = 1.21 - 1 = 0.21
df = f ' (1)dx =(2x|x=1 )(0.1) = (2)(0.1) = 0.20
La variación real difiere de la aproximada en una centésima.
Observación: El punto xo + h es un punto cercano a xo, que se encuentra a la derecha de éste si h es positivo y a la izquierda si h es negativo. En el siguiente ejemplo consideraremos un incremento negativo.
b) Para f(x) = x2 se cumple que D f @ df en xo = 1 y h = -0.1
Solución:
D f = f(0.9) - f(1) = 0.81 - 1 = -0.19
df = f ' (1)dx =(2x|x=1 )(-0.1) = (2)(-0.1) = -0.20
La variación real difiere de la aproximada en una centésima..
c) Para f(x) = x2 se cumple que D f @ df en xo = 2 y h = 0.006
Solución:
D f = f(2.006) - f(2) = 4.024036 - 4 = 0.02403
df = f ' (2)dx =(2x|x=2 )(0.006) = (4)(0.006) = 0.02400
La variación real difiere de la aproximada en tres cienmilésimas
.
d) Para f(x) =
se cumple que D f @ df en xo = 8 y h = 0.2
Solución:
D f = f(8.2) - f(8) = 2.016529 - 2 = 0.016529
df = f ' (8)dx =(
|x=8 )(0.2) = (1/12)(0.2) = 0.016666
La variación real difiere de la aproximada en una diezmilésima.
e) Para f(x) =
Solución:
D f = f(64.2) - f(64) = 4.004162334 - 4 = 0.004162334
df = f ' (649)dx =(
La variación real difiere de la aproximada en cuatro millonésimas.
f) Para f(x) = sen(x) se cumple que D f @ df en xo = p /3, h = 0.1
Solución:
D f = f(p /3 + 0.1) - f(p /3) = 0.9116155 - 0.8660254 = 0.04559
df = f ' (p /3)dx =(cos(x)|x=p /3 )(0.1) = (0.5)(0.1) = 0.050
La variación real difiere de la aproximada en cinco milésimas.
Observación: En todos los ejemplos anteriores comprobamos que D f @ df en el punto e incremento dados, sin embargo tanto D f como df son muy pequeños, casi iguales a cero, y decir que éstos son muy parecidos parece trivial. En realidad éstos dos números son muy parecidos en el sentido de que
como se puede apreciar en el siguiente desarrollo
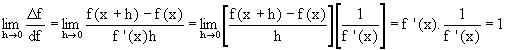
lo cual significa que, para valores muy pequeños de h, la fracción es prácticamente igual a 1 ó bien que D f es prácticamente igual a df.
APLICACIONES DEL DIFERENCIAL
PROBLEMAS DEL TIPO I.
A continuación desarrollaremos algunos ejemplos de aplicación práctica en los que, por medio del diferencial, estimaremos un aumento ó una disminución en alguna función.
Ejemplo 1. Al calentar una placa cuadrada metálica de 15 cm de longitud, su lado aumenta 0.04 cm. ¿Cuánto aumentó aproximadamente su área?.
Solución: Con el fin de ilustrar una situación que se presentará en todos los demás problemas y por la simplicidad de éste en particular, sólo en este caso calcularemos la diferencia de áreas D A y la compararemos con dA.
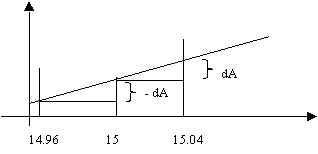
Nótese que originalmente teníamos una placa de 15 x 15, después de calentarla tenemos la placa de 15.04 x 15.04, como se muestra en la figura.
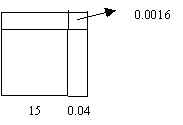
En este caso la función es A(L) = L2 y por lo tanto D A en L = 15 y h = 0.04 es:
A(15.004) - A(15) = 226.2016 - 225 = 1.2016
Si ahora calculamos el diferencial de área para A(L) = L2 en L = 15 y dL = 0.04, obtenemos:
dA = A' (L)dL = (2L)dL =(2L|L=15)(0.004) = (30)(0.004) = 1.2
En consecuencia, cuando el lado se incrementa en 0.4 cm, el área aumenta aproximadamente 1.2 cm2. (El valor exacto del incremento es 1.2016)
Generalmente este tipo de variaciones se miden en porcentajes, es decir, como 0.04 es el 0.2666% de 15 y 1.2 es el 0.5333% de 225 = (15)2, decimos que si el lado de la placa se incrementa en un 0.266%, el área se incrementará aproximadamente en un 0.5333%.
Observación: Si el problema es de una placa metálica del mismo tamaño que se enfría 0.04 cm, entonces h = -0.04 y el diferencial resultaría el mismo sólo que con signo contrario, es decir dA = -1.2. Como estamos usando la recta tangente para estimar la diferencia, la linealidad hace que el cateto opuesto en ambos triángulos de la figura, sean iguales
Resolvamos ahora el mismo problema con otros datos expresados porcentualmente
Ejemplo 2. Al enfriar una placa cuadrada metálica de 20 cm de longitud, su lado disminuye un 0.03%. ¿Cuánto disminuirá porcentualmente su área?.
Solución: El 0.03% de 20 es 
, por
lo que en este caso:
A(L) = L2 , Lo = 20 y dL = -0.006
D A @ dA = 2LdL = 2(20)(-0.006) = (40)(-0.006) = -0.24
Podemos calcular que 0.24 representa el 0.06% de (20)2, por lo que, cuando el lado disminuye un 0.03%, el área disminuye aproximadamente un 0.06%, es decir se duplica porcentualmente.
Este último resultado lo podemos obtener directamente de la siguiente manera:
D A @ dA = 2LdL = 2(20)[
] = 
que representa el 0.06% del área original (20)2.
En general se da esta situación, como se aprecia en el siguiente ejemplo que se deja como ejercicio para el estudiante.
Ejemplo 3. Pruebe que si al calentar (enfriar) una placa cuadrada metálica de lado L, su lado se incrementa (disminuye) un p%, entonces el área se incrementa (disminuye) un 2p%.
Ejemplo 4. La pared lateral de un depósito cilíndrico de radio 50 cm y altura 1 m, debe revestirse con una capa de concreto de 3 cm de espesor. ¿Cuál es aproximadamente la cantidad de concreto que se requiere?
Solución: La cantidad de concreto requerida es la diferencia D V entre el volumen del cilindro exterior y el cilindro interior.
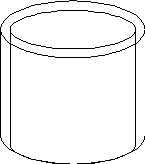
Estimaremos D V por medio de dV, donde V(r) = 100p r2, r = 50, dr =3
dV = (200p r|r=50)(3) =30,000p = 94247.779 cm3
PROBLEMAS DEL TIPO II.
En los siguientes ejemplos utilizaremos el diferencial para estimar errores en la medición de algunas magnitudes.
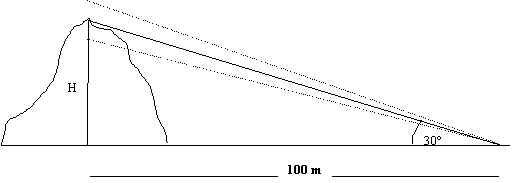
Ejemplo 1. Al calcular la altura de un cerro se encuentra que desde un punto situado a 100m de la proyección en el suelo de la parte más alta del cerro, esta última se ve con un ángulo de elevación de 30º. Encuentre aproximadamente el mayor error que se comete al calcular la altura, sabiendo que la medición del ángulo se hace con un posible error de 0.3º.
Solución: Llamémosle H a la altura del cerro.
En la figura de abajo, 
, por lo que H =(100) tan30º.
Nótese que si el ángulo se mide con un posible error de 0.3º,
estamos diciendo que el valor real del ángulo estará entre 29.7º
y 30.3º, es decir el error en la medición del ángulo sería de
0.3º.
En este caso consideraríamos a H como función de q , es decir:
H(q ) = (100)tanq con q variando entre 29.7º y 30.3º
Para estimar el error D H = H(q ) - H(30º), calcularemos 
, pues q puede tomar valores menores o mayores que
30º.
En este caso q = p /6 y dq = p (0.3)/180 = 0.005235987 (Convertimos grados a radianes)
D H @ dH = (100)H'(q )dq = (100)sec2q dq =(100)(1.3333)(0.005235987) = 0.6981317
En consecuencia si se comete un error máximo de 0.3º en la medición del ángulo, la altura se obtendría con un error máximo de 0.666 m. Se deja como ejercicio comprobar este resultado evaluando directamente D H
PROBLEMAS DEL TIPO III.
A continuación utilizaremos el diferencial para calcular valores aproximados de funciones.
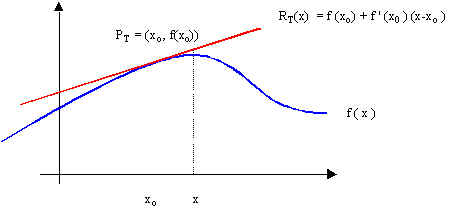
Cuando estudiamos a la recta tangente como la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia PT, aprovechamos la simplicidad de la ecuación de una recta para aproximar con ésta, otro tipo de funciones no tan sencillas.
Obsérvese que en la gráfica, f (x) 
RT(x) para valores x "cercanos" a xo.
Ejemplo 1: Encuentre un valor aproximado para, 
utilizando la recta tangente.
Solución:
Encontremos pues la ecuación de la recta tangente a la gráfica
de 
en (16 , 4), es decir la ecuación de la recta que
pasa por (16 , 4) y tiene pendiente f ' (16).
f '(x) = 
y por lo tanto f '(16)
= 0.125
Así pues la ecuación buscada es y = RT(x) = 4 + 0.125 (x - 16)
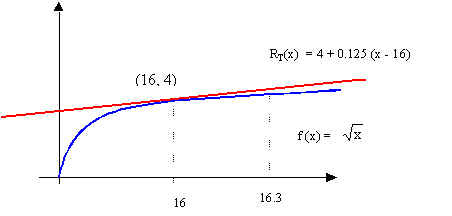
Como el punto 16.3 está "muy próximo" a 16, en vez de evaluar f (16.3), evaluamos RT(16.3), obteniendo:
Así pues 
Nótese que si comparamos con el valor que nos da la
calculadora, 
= 4.0373 , nuestra aproximación es
buena hasta dos diezmilésimas, lo cual puede resultar suficiente
para cientos fines prácticos. Cuando estudiemos El Teorema de
Taylor, seremos capaces de obtener la aproximación con el grado
de precisión deseado.
Observación: En la ecuación de la recta tangente en el punto (xo , f(xo))
RT(x) = f (xo ) + f ' (xo ) (x-xo )
Si tomamos x = xo + h, tendremos la expresión:
RT(x) = f (xo ) + f ' (xo ) h
Y si sustituimos f '(xo)h = df, obtendremos:
RT(x) = f (xo ) + df.
Como sabemos que para valores de x cercanos a xo, f(x) @ RT(x), obtenemos:
f(x) @ f (xo ) + df
Este resultado lo podemos expresar de la siguiente manera:
Podemos estimar el valor de f en x, cercano a xo, agregándole a f (xo) el diferencial correspondiente.
Observación. Nótese que es necesario conocer el valor de f y de su derivada en el punto x0.
En el ejemplo anterior tendríamos los siguiente datos:
a)
b) xo = 16
c) x = 16.3
d) dx = 0.3
Con estos datos, df = (|x=16) (0.3)
= 0.0375, y por lo tanto:
+ 0.0375 = 4.0375.
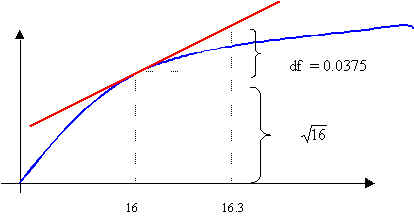
Gráficamente lo que estamos haciendo es evaluar a 16.3 en la recta tangente, como se aprecia en la gráfica anterior que aquí presentamos amplificada.
Ejemplo 2. Utilizando diferenciales, encuentre un valor
aproximado para 
Solución: Resumiendo lo anteriormente expuesto:
@ 
+ df
donde:
a)
b) xo = 32
c) x = 32.8
d) dx =0.8
f ' (x) = 
, por lo que f ' (32) =
1/80 = 0.0125
y por lo tanto df = (0.0125)(0.8) = 0.01.
Así pues @
2.01.
Ejemplo 3. Utilizando diferenciales, encuentre un valor aproximado para sen31.5º
Solución:
Sen31.5º @ sen30º + df
Donde
a) f(x) = senx
b) xo = p /6 medida en radianes de 31º
c) x = p /6 + 1.5(p /180) medida en radianes de 31.5º
d) dx = 1.5(p /180) medida en radianes de 1.5º
f '(x) = cosx, por lo que f '(p /6) = cos(p /6) = 0.86660254
y por lo tanto df = (0.8660254)(1.5)(p /180) = (0.8660254)(0.026179) = 0.02267
Así pues sen(31.5º) @ 0.5 + 0.02267 = 0.52267
Sen(31.5º) @ 0.52267
PROBLEMAS DEL TIPO IV.
Utilización del diferencial para estimar cambios de una variable con respecto a otra sin explicitar las variables dependiente e independiente.
Ejemplo 1. La Ley de Boyle para la expansión de un gas encerrado es PV = C, donde P es la presión expresada como el número de libras por unidad de área, V es el volumen del gas y C es una constante. Demuestre que si la ley de Boyle se cumplen entonces VdP + PdV = 0
Solución. En este tipo de situaciones tenemos dos posibilidades para establecer una función: a P como función de V ó a V como función de P.
Supondremos que P ó V son diferentes de cero, ya que en caso contrario trivialmente se cumple lo que queremos probar.
a) Forma 1: Supongamos que V ¹ 0 y consideremos a P como función de V.
De la ley de Boyle, despejamos P en términos de V:
ó bien 
,
calculamos el Diferencial de P en el punto V con un incremento dV y obtenemos:
de nuevo de la Ley de Boyle sabemos que y si
lo sustituimos en la expresión para dP, obtenemos:
pasamos multiplicando a V de la última a la primera expresión de la igualdad anterior, obteniendo
VdP = -PdV ó bien VdP + PdV = 0.
b) Forma 2: Supongamos que P ¹ 0 y consideremos a V como función de P.
De la ley de Boyle, despejamos V en términos de P:
(no hacemos explícita a la variable independiente)
calculamos el Diferencial de V en el punto P con un incremento dP y obtenemos:
de nuevo de la Ley de Boyle sabemos que 
y si
lo sustituimos en la expresión para dP, obtenemos:
obteniendo también la expresión deseada PdV + VdP = 0
Ejemplo 2. La resistencia eléctrica R de un conductor (cable) es directamente proporcional a su longitud e inversamente proporcional al cuadrado de su diámetro. Suponiendo que la longitud es constante, ¿con qué precisión debe medirse el diámetro (en términos del error porcentual) para mantener el error porcentual de R entre -3% y 3%?
Solución. 
Nos piden calcular dD sabiendo que dR = (0.03)R
despejando dD, obtenemos:
como 
En consecuencia el diámetro debe medirse con una precisión del 1.5%.
Ejemplo 3. Si el error posible en la medición del volumen de un gas es de 0.1 pie3 y el error permitido en la presión es de (0.001)C lb/pie2, determine el tamaño del recipiente más pequeño para el cual se cumple la ley de Boyle.
Solución. Si la ley de Boyle ha de cumplirse, debe pasar que VdP + PdV = 0, de donde despejando V, obtenemos:
De acuerdo a los datos dP varía de -(0.001)C lb/pie2 a (0.001)C lb/pie2 y dV varía de -(0.1) pie3 a 0.1 pie3.
La expresión dentro del radical, fuerza a que uno de los dos diferenciales sea negativo y para que la fracción sea lo más pequeña posible, el numerador debe ser lo más pequeño y el denominador lo más grande posible, consiguiéndose esto con dV = -0.1 y dP = (0.001)C.
V =
Por lo que el recipiente debe ser de 10 pie3.
